




Next: EXPERIMENTS
Up: RESIDUAL MIGRATION OPERATOR
Previous: Kinematic relations
To use a finite-difference approach, we need to derive formulas for
partial derivatives:
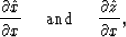
or
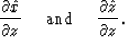
Let us first simplify notations by denoting

and
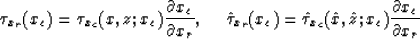
where xc=xs or xr. Now we define
| 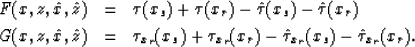 |
(6) |
| (7) |
Then, equation (5) becomes
| 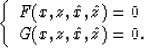 |
(8) |
Taking partial derivative with respect to x
on both sides of equation (8) gives:
| 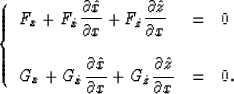 |
(9) |
Similarly, taking partial derivative with respect to z yields
| 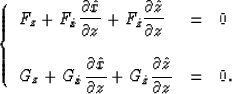 |
(10) |
In matrix notations, these equations become:
| 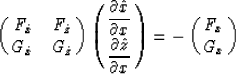 |
(11) |
| 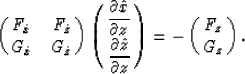 |
(12) |
Solving these linear equation sets analytically, we can obtain two sets
of partial differential equations for 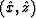 ,
,
| 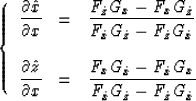 |
(13) |
and
| 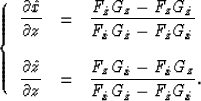 |
(14) |
On the right hand side of these equations,
we have the partial derivatives of F and G. These partial derivatives
are related to the partial derivatives of traveltimes. From equations
(6) and (7), we can derive:
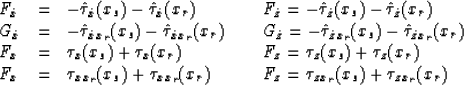
Because the upwind finite-difference algorithm calculates accurate
traveltimes on a regular grid, I use this trave-time table to
compute the derivatives of traveltimes, and in turn to compute
the expressions on the right hand side of equations
(13) and (14). Therefore, equations
(13) and (14) become linear partial differential
equations and are easy to be solved by many existing numerical algorithms.
I use the leapfrog method, in which a partial derivative is taken as
a difference between two neighboring points:
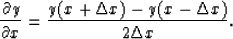
To obtain an initial solution, I use searching method
to find the operator at some point. The finite-difference algorithm can then
calculate the operators elsewhere, and step by step.





Next: EXPERIMENTS
Up: RESIDUAL MIGRATION OPERATOR
Previous: Kinematic relations
Stanford Exploration Project
1/13/1998
![]()
![]()
![]()
![]()
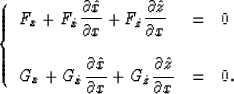
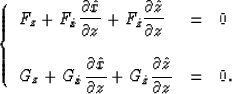
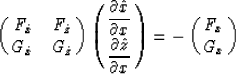
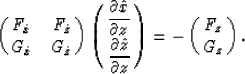
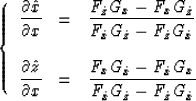
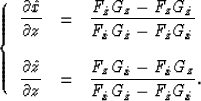
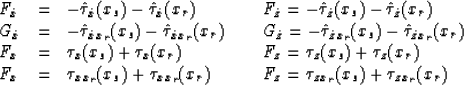
![]()