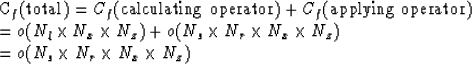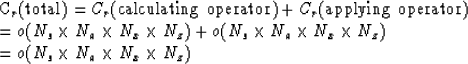next up previous print clean
Next: Kinematic relations Up: RESIDUAL MIGRATION OPERATOR Previous: RESIDUAL MIGRATION OPERATOR

Computational costs

I compare the computational costs of full migration and residual migration under the assumption that they are implemented with the Kirchhoff integral in the common shot geometry. I omit those costs that do not depends on the dimensions of data.

A Kirchhoff migration can be done in two steps: (1) calculating operators and (2) applying operators. Suppose a dataset consists of Ns shot gathers. In each shot gather, there are Nr receivers. The image we try to obtain from this dataset has a dimension of 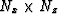$N_x\times N_z$. Then, the computational cost of full migration is
\begin{eqnarraystar} C_f(\hbox{total}) & = & C_f(\hbox{calculating operator})+C_... ...times N_z) \\ & = & o(N_s\times N_r \times N_x\times N_z) \\ \end{eqnarraystar}
where Nl< Ns+Nr is the number of surface locations sampled by the experiment, and the small letter o stands for order.

The computational cost of residual migration is
\begin{eqnarraystar} C_r(\hbox{total}) & = & C_r(\hbox{calculating operator})+C_... ...\times N_z) \\ & = & o(N_s\times N_a\times N_x\times N_z) \\ \end{eqnarraystar}
where Na is the number of samples required to represent residual-migration operators. Because the aperture of a residual-migration operator is usually much smaller than that of a full-migration operator, Na is much smaller than Nr, which makes the application of residual migration efficient. From this comparison, we see that, in full migration, applying operators is the major consumer of the computation-time. In residual migration, however, calculating residual-migration operators is computationally more expensive than applying operators. Therefore, efforts should be made on reducing the cost of calculating residual-migration operators.

next up previous print clean
Next: Kinematic relations Up: RESIDUAL MIGRATION OPERATOR Previous: RESIDUAL MIGRATION OPERATOR
Stanford Exploration Project
1/13/1998