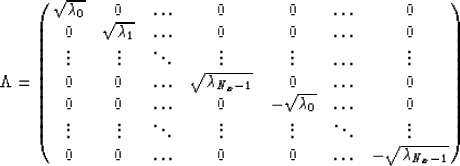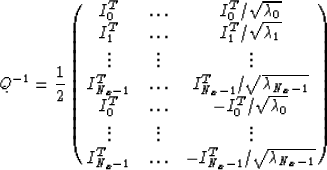Next: Arbitrary velocity structures
Up: THE GENERALIZED PHASE-SHIFT METHOD
Previous: THE GENERALIZED PHASE-SHIFT METHOD
The 2Nx by 2Nx matrix A can be partioned according to
| ![\begin{displaymath}[A]
=\pmatrix{0 & I_{N_x}\cr A_{21} & 0}\end{displaymath}](img10.gif) |
(5) |
where INx denotes the Nx by Nx identity matrix and
the Nx by Nx submatrix A21 is given by
| ![\begin{displaymath}[A_{21}]
=\pmatrix{-{\omega^2 \over c^2}-{\partial^2 \over \p...
... \ldots &-{\omega^2\over c^2}-{\partial^2 \over \partial x^2} }\end{displaymath}](img11.gif) |
(6) |
The horizontal discretization requires an approximation for the derivative
term in equation (6). As with the ordinary phase-shift method (Gazdag, 1978),
this derivative can be calculated by Fourier method
| 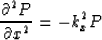 |
(7) |
Since multiplication in the space domain is equivalent to convolution in the
wavenumber domain, the multiplication of the sloth (squared slowness) becomes
convolution. For horizontally uniform structures, however, the Fourier
transform of the velocity function is a delta function. Therefore, the
submatrix A21 has the form
| ![\begin{displaymath}[A_{21}]
=\pmatrix{-{\omega^2 \over c^2}+k_x^2 & 0 & \ldots &...
...dots & \vdots \cr
0 & 0 & \ldots &-{\omega^2\over c^2}+k_x^2 }\end{displaymath}](img13.gif) |
(8) |
The diagonal elements of this matrix are the eigenvalues of A21 and
a matrix in which the columns consist of the eigenvectors form an identity
matrix.
By letting the eigenvalues of submatrix A21 as
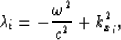
the eigenvalues of matrix A become 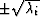 , for i=1,...,Nx-1.
The corresponding eigenvectors are given by
, for i=1,...,Nx-1.
The corresponding eigenvectors are given by
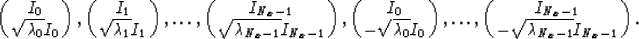
where Ii denotes i-th column of identity matrix.
With these eigenvectors we define a 2Nx by 2Nx matrix Q in which
the columns consist of the eigenvectors of A. We then have the relation
| 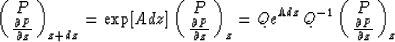 |
(9) |
where 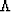 is the diagonal matrix
is the diagonal matrix
| 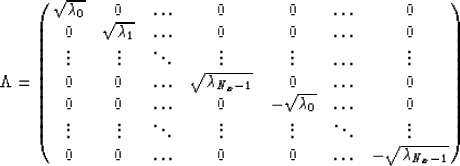 |
(10) |
and
| 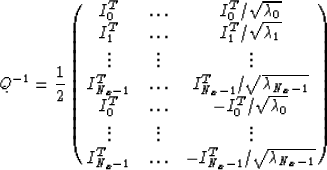 |
(11) |
When both sides of equation (9) are multiplied by Q-1 from the left we
obtain
| ![\begin{displaymath}
Q^{-1}\pmatrix{P\cr {\partial P\over \partial z}}_{z+dz} = \...
...bda dz}]Q^{-1} \pmatrix{P\cr {\partial P\over \partial z}}_{z} \end{displaymath}](img21.gif) |
(12) |
The equation (12) is a matrix representation for a set of equations
| 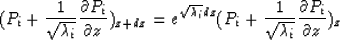 |
(13) |
and
| 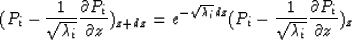 |
(14) |
The solutions of equations (13) and (14) represent upgoing and downgoing waves
respectively.
When an eigenvalue 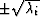 is real, the component is propagated
by a multiplication by a real exponential, and results in an evanescent
component which should be removed for numerical stability. When an eigenvalue
is real, the component is propagated
by a multiplication by a real exponential, and results in an evanescent
component which should be removed for numerical stability. When an eigenvalue
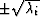 is imaginary, the corresponding coefficient is
propagated by phase shift.
is imaginary, the corresponding coefficient is
propagated by phase shift.





Next: Arbitrary velocity structures
Up: THE GENERALIZED PHASE-SHIFT METHOD
Previous: THE GENERALIZED PHASE-SHIFT METHOD
Stanford Exploration Project
1/13/1998
![\begin{displaymath}[A_{21}]
=\pmatrix{-{\omega^2 \over c^2}-{\partial^2 \over \p...
... \ldots &-{\omega^2\over c^2}-{\partial^2 \over \partial x^2} }\end{displaymath}](img11.gif)
![\begin{displaymath}[A_{21}]
=\pmatrix{-{\omega^2 \over c^2}+k_x^2 & 0 & \ldots &...
...dots & \vdots \cr
0 & 0 & \ldots &-{\omega^2\over c^2}+k_x^2 }\end{displaymath}](img13.gif)
![]()
![]()