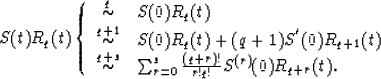Let ![]() , then:
, then:
![]()
| |
(10) |
Let us prove the last formula. We must prove that ![]() is a continuous function:
is a continuous function:
![\begin{eqnarray}
{\bf D}^{q}[\cdot ]& = & {\bf D}^{q} \{[S(t) - S(0)] R_{q}(t) \...
...{S^{'}(t) R_{q}(t) \} + {\bf D}^{q-1}\{ [S(t)-S
(0)]R_{q-1}(t) \}.\end{eqnarray}](img79.gif) |
(11) | |
| (12) | ||
| (13) |
The last term has the sharpest discontinuity , so we needn't pay any attention to the first one. Repeating the procedure we get at the end the sharpest term:
[S(t)-S(0)]R0(t)
which is continuous at the point t=0.Instead of equation (10), we may derive a more general formula: