




Next: Hilbert transformation
Up: 2: THE STANDARD DISCONTINUITIES
Previous: Examples
It is obvious that the integration of Rq(t) gives Rq+1(t):
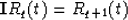
and in general:
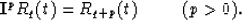
Does it imply that: 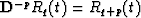 (where
(where 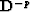 is the inverse
of
is the inverse
of 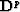 )? If we apply the operator
)? If we apply the operator 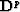 to the sum Rp+q(t)+Pn(t),
we get for
to the sum Rp+q(t)+Pn(t),
we get for 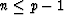 :
:
![\begin{displaymath}
{\bf D}^p[R_{q+p}(t)+P_n(t)]=R_q(t).\end{displaymath}](img93.gif)
But 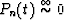 , so:
, so:
| 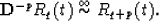 |
(14) |





Next: Hilbert transformation
Up: 2: THE STANDARD DISCONTINUITIES
Previous: Examples
Stanford Exploration Project
1/13/1998
![]()
![]()
![]()