ELASTIC ENERGY STORED IN EQUIVALENT MEDIA

The elastic energy stored in a medium when a force is applied on the exterior boundary is calculated by the double dot product of stress and strain integrated over the whole volume. Using our notation we can calculate the deformation energy in a form that incorporates the layer geometry.

$$H = \oint_V{ { {\epsilon(z)}_{} : {\sigma(z)}_{} } dV = \o... ...)}_{N} \cr} \pmatrix{ {\epsilon}_{T} \cr {\sigma}_{N} \cr} }dV$$ (13)

Thus the total elastic energy H in the medium is given by  

$$H = \oint_V{ \pmatrix{ {\epsilon}_{T} & {\sigma}_{N} \cr} \p... ...{NN} \cr} \pmatrix{ {\epsilon}_{T} \cr {\sigma}_{N} \cr} }dV ~.$$ (14)

We can calculate the energy per unit area for both the heterogeneous and the homogeneous equivalent. If we require that the energy stored in the two media be the same we have the equation,

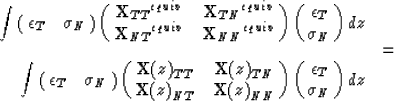$$\begin{eqnarray} \int \pmatrix{ {\epsilon}_{T} & {\sigma}_{N} \cr} \pmatrix{ { ... ...(z)}_{NN} \cr} \pmatrix{ {\epsilon}_{T} \cr {\sigma}_{N} \cr} dz \end{eqnarray}$$ (15)

which leads us to the following expression by taking constant components out of the integrals:

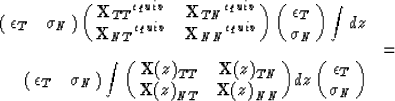$$\begin{eqnarray} \pmatrix{ {\epsilon}_{T} & {\sigma}_{N} \cr} \pmatrix{ { {\bf X... ...z)}_{NN} \cr} }dz \pmatrix{ {\epsilon}_{T} \cr {\sigma}_{N} \cr} &\end{eqnarray}$$ (16)

The requirement of energy equality leads to the same equations as those developed by Schoenberg and Muir. The hybrid matrix of the equivalent medium is the thickness weighted average of the hybrid matrices ${\bf X(z)}_{}$.