Tomography

In seismic tomography, traveltimes recorded in a seismic experiment are compared with traveltimes computed for an assumed velocity model, and their differences are used to predict any anomalies in the model (Dines and Lytle, 1979; Bishop et al., 1985; Nolet, 1987). Tomographic methods generally use an iterative approach, in which many traveltime calculations are needed for the algorithm to converge to the correct solution. Because the calculations are fast and efficient, the finite-difference traveltime method is well-suited for tomography.

 

strmodevt
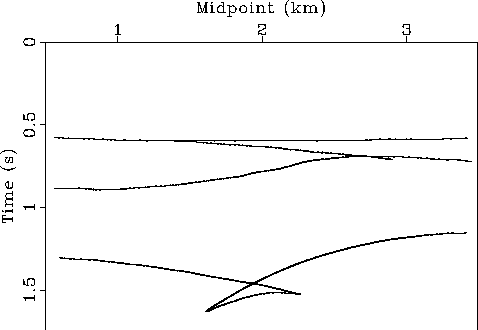
Figure 10 Reflection events in a constant-offset section computed for reflectors in the model of Figure 6. The offset is 1 km.

The application of this method to tomography is not limited to the transmission experiment; reflection traveltimes can be computed by combining information from ``source'' and ``geophone'' traveltime maps. For example, Figure 10 shows the reflection events in a constant-offset section, computed for interfaces in the model of Figure 6. After the calculation of the source and receiver traveltime maps, reflection times are found by the summation of source and receiver times at locations along the interface where Snell's law is satisfied. Incidence and reflection angles at the interface are computed from the traveltime gradients, which are readily available in the finite-difference calculations. When calculations must be done for a large number of regularly spaced sources and geophones, this approach is much more efficient than two-point ray tracing.

Note that no rays are needed in the computation of reflection times. Similarly, in seismic tomography, optimization schemes can be designed that do not require any rays in the calculation of the Jacobian of traveltimes with respect to slowness. We are currently investigating the application of these techniques to migration-velocity analysis (Van Trier, 1989) and reflection tomography (Santosa and Symes, 1989). Vidale and Ammon (1989) also apply the finite-difference traveltime calculations to tomography without using rays. They use a random-search optimization method in the inversion of traveltime perturbations.