|
spitz
Figure 4 Modified Spitz model. Three ideal plane waves with impulsive noise and irregularly spaced missing traces. | 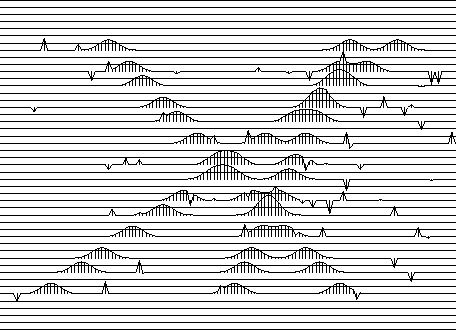 |
|
spitz
Figure 4 Modified Spitz model. Three ideal plane waves with impulsive noise and irregularly spaced missing traces. |  |
Signals that are plotted entirely as zeros are taken to be missing. Besides missing traces on either side are irregularly interleaved zero signals depicting missing traces. Here we set for ourselves the goal of filling in the missing traces in Figure 4 as well as finding the three slopes, p1, p2, and p3.
The problem of finding the wave slopes in data such as Figure 4 is an old one in seismology. A tremendous volume of human intellect has been brought to bear upon it. To begin with, the problem is widely solved using an intuitive approach which is simply the conjugate operator. In other words, the data can be regarded as a superposition of plane waves of all possible angles. The conjugate operation, called ``slant stack'' is to sum the data sample over many angles. Slant stack has an analytical inverse (see for example ``Imaging the Earth's Interior''). The trouble is that theoretical inverse hinges on absence of aliasing and truncation--essential features of Figure 4. A problem with the conjugate is that its resolution is not sharp. When one of the plane waves is much stronger than the others then truncation and aliasing of the strong event can hide the weaker events. The method we'll develop here should be able to see weak events in the presence of strong ones.