|
missif
Figure 1 Top is known data. Middle includes the interpolated values. Bottom is the filter with the leftmost point constrained to be unity. | 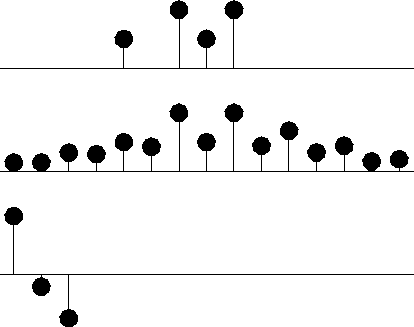 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
There the filters were taken as known
and the unknowns were only the missing data.
Now instead of having a predetermined filter
we'll solve for the filter along with the missing data.
The principle used is that the output power is minimized
while the filter is constrained to have one nonzero coefficient
(else all the coefficients would go to zero).
First we'll look at some results and then see how they were found.
.
There the filters were taken as known
and the unknowns were only the missing data.
Now instead of having a predetermined filter
we'll solve for the filter along with the missing data.
The principle used is that the output power is minimized
while the filter is constrained to have one nonzero coefficient
(else all the coefficients would go to zero).
First we'll look at some results and then see how they were found.
In Figure 1 the filter is constrained to be of the form (1,a1,a2).
|
missif
Figure 1 Top is known data. Middle includes the interpolated values. Bottom is the filter with the leftmost point constrained to be unity. |  |
The result is pleasing in that the interpolated traces
have the same general character as the given values.
The filter came out slightly different from the (1,0,-1)
that I suggested based on a subjective analysis
for Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Curiously, constraining the filter to be of the form (a-2,a-1,1)
in Figure 2
yields the same interpolated missing data as in the previous figure.
.
Curiously, constraining the filter to be of the form (a-2,a-1,1)
in Figure 2
yields the same interpolated missing data as in the previous figure.
|
backwards
Figure 2 Top is known data. Middle includes the interpolated values. Bottom is the filter with the rightmost point constrained to be unity. | 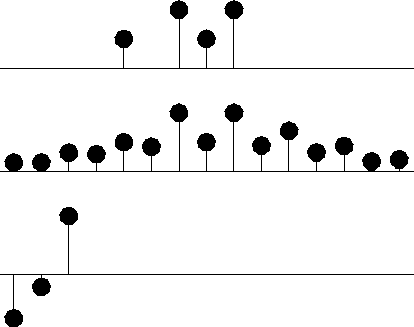 |
I understand the sum squared of the coefficients of A(Z)Y(Z) is the same as that of A(1/Z)Y(Z) but don't see why that would imply the same interpolated data.
Changing the filter constraint to be of the form (a-1, 1, a1) yields a much different interpolation shown in Figure 3. The interpolated data is much smoother than the given data. This is because the missing data is produced from an interpolation-error filter instead of a prediction-error filter. A fact not evident from the figures is that the value of the output power was smaller for interpolation than for prediction. I cannot explain why the filter turned out to be imperceptibly different from a second difference operator, but somewhere I think I have a proof that it is a symmetrical operator.
|
center
Figure 3 Top is known data with missing data represented by zeros. Middle includes the interpolated values. Bottom is the filter. | 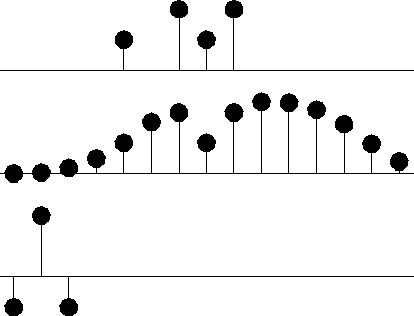 |