




Next: Rate of convergence
Up: CLASH IN PHILOSOPHIES
Previous: CLASH IN PHILOSOPHIES
Let us look at the issue of ``relying on data not paid for''.
First we'll see
that interpolation and extrapolation need do no harm.
Conventional inversion can be expressed by minimizing the quadratic form
| 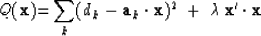 |
(4) |
where
 is the model vector,
is the model vector,
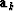 is the kth row of a partial derivative matrix,
dk is the kth known data point,
is the kth row of a partial derivative matrix,
dk is the kth known data point, 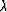 is a scalar,
and to avoid clutter I have neglected the residual weighting.
The missing data philosophy
is to add terms involving the missing data dm, namely
is a scalar,
and to avoid clutter I have neglected the residual weighting.
The missing data philosophy
is to add terms involving the missing data dm, namely
| 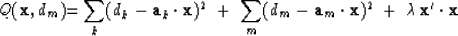 |
(5) |
Since the missing data dm are freely adjusted variables,
it is evident that the value of Q at the minimum is the same
both with and without the missing data.
Missing data interpolated or extrapolated in this way
cannot perturb the solution  .Of course there are many other ways to interpolate and extrapolate,
and they are generally less sophisticated than the model-based
method I am describing.
How can they be of value?
.Of course there are many other ways to interpolate and extrapolate,
and they are generally less sophisticated than the model-based
method I am describing.
How can they be of value?





Next: Rate of convergence
Up: CLASH IN PHILOSOPHIES
Previous: CLASH IN PHILOSOPHIES
Stanford Exploration Project
1/13/1998