




Next: Does it work?
Up: INTERPOLATION WITH P.D.E. DIP
Previous: Spatial interpolation with
You can reject two dips with the operator
| 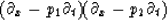 |
(1) |
Finding the two values p1 and p2 is a nonlinear problem
that is easy.
Let u be the input signal and v be the output signal.
Consider
| 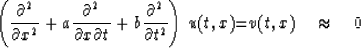 |
(2) |
Now recognize that (2)
(which is a separate equation at each point in the (t,x) space of v(t,x))
is an overdetermined set of linear equations
for the two unknowns a and b.
It is easy to find a and b which by comparison
with equation (1)
gives p1 and p2 by the nonlinear but easy equations
a=p1+p2 and b=p1p2.
The minimum signal required is three seismograms
(on which to express 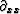 ).
).
To recapitulate,
first a simple procedure gives us the required coefficients
for a filter that fits two waves to the dataset u(t,x).
Second, the same dip filter coefficients can be applied
on a mesh in which t and x are interleaved,
thus introducing new data locations on which we need data.
Third, we interpolate t by any method.
Fourth, we find missing traces by minimizing the power in v(t,x).





Next: Does it work?
Up: INTERPOLATION WITH P.D.E. DIP
Previous: Spatial interpolation with
Stanford Exploration Project
1/13/1998