




Next: Inverse transformation
Up: EXPRESSIONS OF THE PARABOLIC
Previous: EXPRESSIONS OF THE PARABOLIC
The modeling equation is similar to Thorson's equation for hyperbolic
transforms. It expresses the NMO-corrected data d(t,h) as a function
of the field U in the t0-p domain:
| ![\begin{displaymath}
d(t,h)=\sum_{t_0}\sum_p U(t_0,p)\delta[t_0-(t-ph^2)]\end{displaymath}](img4.gif) |
(3) |
whereas, for Thorson's equation, the 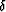 term has to be replaced by
term has to be replaced by
![$\delta\!~[~t_0~-~\sqrt{t^2-p^2h^2}~]$](img6.gif) . Similarly, it can be compared to the
slant-stack modeling:
. Similarly, it can be compared to the
slant-stack modeling:
![\begin{displaymath}
d(t,h)=\sum_{\tau}\sum_p U(\tau,p)\delta[\tau-(t-ph)]\;. \end{displaymath}](img7.gif)
Equation (3) will transform a spike in the t0-p domain
into a parabola (or straight line if p=0) in the time-offset domain.
I symbolize equation (3) as: d=L.U. Equation (3)
can be expressed in the frequency domain. For the 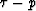 transform,
Kostov (1989) showed that:
transform,
Kostov (1989) showed that:
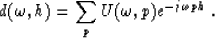
For the parabolic transform, we get:
| 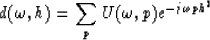 |
(4) |
So, for a fixed 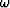 , an element of the matrix L is:
, an element of the matrix L is:
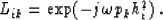
Stacking along parabolas actually corresponds to computing
U=LT.d (as Thorson pointed out in the case of hyperbolic stacking). We
will transform the data d(t,h) into the t0-p domain by using the
least-squares inverse of L, i.e. (LTL)-1LT in the overdetermined
case (or LT(LLT)-1 in the underdetermined case):
| 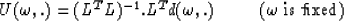 |
(5) |





Next: Inverse transformation
Up: EXPRESSIONS OF THE PARABOLIC
Previous: EXPRESSIONS OF THE PARABOLIC
Stanford Exploration Project
1/13/1998
![]()
![]() transform,
Kostov (1989) showed that:
transform,
Kostov (1989) showed that:
![]()
![]()