




Next: CONCLUSION
Up: EXAMPLE: MULTIPLES REMOVAL
Previous: Results on the data
Actually, I came to the idea of the Burg-type algorithm when I noticed
the instability of the LSL algorithm. But I still tried to improve the LSL
method. Particularly noticing the lack of lateral continuity,
I tried to derive a multichannel formalism. Actually, the
formalism developed by Friedlander (1982) is a multichannel formalism.
It still estimates the optimal residuals for each trace,
as though we wanted to estimate one optimal filter for each trace.
However, it considers also the correlations between traces. For example,
if we have m traces, the covariances Rr, 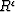 , and
, and 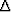 are
are 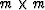 matrices, and the algorithm would require the inversion
of these
matrices, and the algorithm would require the inversion
of these 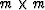 matrices at each iteration! As you see, it would
be extremely fastidious and impractical to implement such an algorithm,
as soon as we have more than 4 or 5 traces.
matrices at each iteration! As you see, it would
be extremely fastidious and impractical to implement such an algorithm,
as soon as we have more than 4 or 5 traces.
Because of this difficulty, I tested multichannel procedures similar to
Burg's multichannel processing, in which we average the reflection coefficients
along offset. Different
averagings can be used: either the coefficients themselves, or their numerators
and denominators separately, or even median filtering (Woodward and Dellinger,
1984). But, when applied to the LSL algorithm, these procedures simply don't
work, because the time-update recursions cannot be averaged. The reflection
coefficients quickly become larger than 1, and the algorithm ``explodes''.
However, this kind of multichannel processing can be applied to my Burg-type
algorithm, as in the exact Burg (non-adaptive) algorithm, by averaging
the numerators and denominators of the reflection coefficients.





Next: CONCLUSION
Up: EXAMPLE: MULTIPLES REMOVAL
Previous: Results on the data
Stanford Exploration Project
1/13/1998