




Next: Results on the data
Up: EXAMPLE: MULTIPLES REMOVAL
Previous: EXAMPLE: MULTIPLES REMOVAL
In this case, we are trying to predict the data sequence xT from its lagged
past values. To do that, we are minimizing:
![\begin{displaymath}
\sum_{t=0}^T(\varepsilon_{n,T}(t))^2=\sum_{t=0}^T[x(t)-f_{n,1}x(t-L)-\cdots-f_{n,n}x(t-L-(n-1))]^2 \;.\end{displaymath}](img100.gif)
L is the lag of the prediction. So we can apply my adaptive
algorithms, taking yT=ZLxT, or y(t)=x(t-L). To have an adequate
prediction model, I take a marine shot-gather, where I will try to
remove the water-bottom multiples and peglegs. L should be the
two-way traveltime in the water trench.
However, the prediction model is not adequate in the time-offset domain,
because the lag of the water-bottom multiples is not constant on a non-0 offset
trace. Actually, this lag is a function of the angle of incidence 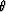 of
the wavefront at the receiver. As the parameter
of
the wavefront at the receiver. As the parameter 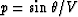 is constant
along a ray, this lag depends only upon the p-parameter of the incident ray.
So, to make the prediction model more appropriate, it is better to transform
the data to the
is constant
along a ray, this lag depends only upon the p-parameter of the incident ray.
So, to make the prediction model more appropriate, it is better to transform
the data to the 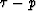 domain with a slant-stack transform, and apply
the prediction process in this domain.
domain with a slant-stack transform, and apply
the prediction process in this domain.
Calling VW the water velocity, the variation of the lag L with the
p-parameter is given by the relationship:
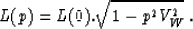
Thus, after having transformed the input gather to the 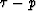 domain,
I will apply the adaptive algorithms on each trace, with yT=ZLxT,
and L given by the previous relation. However, I recognize that this method
should not be efficient for large p-parameters, because the lag L will be
very small (close to 1): the process will try at the same time to remove the
multiples and to compress the signal. But for my purpose, which is a comparison
between different adaptive methods, I consider it is sufficient.
domain,
I will apply the adaptive algorithms on each trace, with yT=ZLxT,
and L given by the previous relation. However, I recognize that this method
should not be efficient for large p-parameters, because the lag L will be
very small (close to 1): the process will try at the same time to remove the
multiples and to compress the signal. But for my purpose, which is a comparison
between different adaptive methods, I consider it is sufficient.





Next: Results on the data
Up: EXAMPLE: MULTIPLES REMOVAL
Previous: EXAMPLE: MULTIPLES REMOVAL
Stanford Exploration Project
1/13/1998
![\begin{displaymath}
\sum_{t=0}^T(\varepsilon_{n,T}(t))^2=\sum_{t=0}^T[x(t)-f_{n,1}x(t-L)-\cdots-f_{n,n}x(t-L-(n-1))]^2 \;.\end{displaymath}](img100.gif)
![\begin{displaymath}
\sum_{t=0}^T(\varepsilon_{n,T}(t))^2=\sum_{t=0}^T[x(t)-f_{n,1}x(t-L)-\cdots-f_{n,n}x(t-L-(n-1))]^2 \;.\end{displaymath}](img100.gif)
![]() of
the wavefront at the receiver. As the parameter
of
the wavefront at the receiver. As the parameter ![]() is constant
along a ray, this lag depends only upon the p-parameter of the incident ray.
So, to make the prediction model more appropriate, it is better to transform
the data to the
is constant
along a ray, this lag depends only upon the p-parameter of the incident ray.
So, to make the prediction model more appropriate, it is better to transform
the data to the ![]() domain with a slant-stack transform, and apply
the prediction process in this domain.
domain with a slant-stack transform, and apply
the prediction process in this domain.
![]()