![]()
| |
(16) |
![\begin{displaymath}
{\cal E}^{x}(K^x_k)\ =\sum_{t=0}^{T_{max}-1}\lambda^{\vert T...
...ert T-t\vert}[\varepsilon^x_{k-1}(t)-K^x_{k}r_{k-1}(t-1)]^2 \;.\end{displaymath}](img97.gif)
As I already said, this expression of the energy forces the residuals to depend on past and future data, because the summation symbol extends to the whole time window. But the formalism is still adaptive, because the weighting is non-uniformly centered around the time of interest T. The minimization with respect to Kxk leads to the expression:
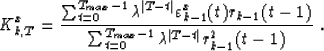 |
(17) |
The denominator is indeed the one involved in the computation of the reflection coefficient Krk,T, and we already saw how we can compute it recursively. The numerator can also be split into past and future summations Nx-k(t) and Nx+k(t) verifying:
| |
(18) |
In conclusion, the idea of the algorithm is to perform at the same time an adaptive self-prediction of the data y(t) with my modified version of Burg's adaptive algorithm, and the adaptive prediction of x from y with the recursions derived in this section. The self-prediction of y is processed with the recursion formulas (13), (15), and (16). The prediction of x is performed with the recursions (17), (18), and (19).