




Next: Conclusion
Up: THE LSL ALGORITHM
Previous: Statistical signification of
We are interested in the prediction of a time series
xT from a related process yT. We want to minimize:
![\begin{displaymath}
\sum_{t=0}^T (\varepsilon^x_{n,T}(t))^2 = \sum_{t=0}^T [x(t)-f_{n,T}(1)y(t-1)-\cdots-f_{n,T}(n)y(t-n)]^2\;.\end{displaymath}](img63.gif)
Once again, we are interested only in the residual 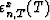 , so that
the residuals are affected only by past values, and not by future values.
This minimization problem leads to:
, so that
the residuals are affected only by past values, and not by future values.
This minimization problem leads to:
If we are interested in the residuals 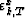 themselves, then
we have to find the orthogonal complement of xT
on the space
themselves, then
we have to find the orthogonal complement of xT
on the space 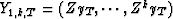 . So, the idea is
to use the backward residuals of the self-prediction of yT
to form an orthogonal basis of the space Y1,k,T, and then
project the vector xT onto this particular basis.
Consequently, we will lead two recursions at the same time:
one to compute the variables
. So, the idea is
to use the backward residuals of the self-prediction of yT
to form an orthogonal basis of the space Y1,k,T, and then
project the vector xT onto this particular basis.
Consequently, we will lead two recursions at the same time:
one to compute the variables 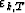 and rk,T of the
self-prediction of yT, and the other to compute the residuals
and rk,T of the
self-prediction of yT, and the other to compute the residuals
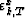 of the joint prediction of xT from yT.
of the joint prediction of xT from yT.
The order-updating of the residuals 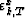 is very similar
to the updating of the residuals
is very similar
to the updating of the residuals 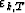 . Effectively,
. Effectively,
| 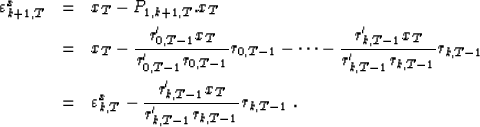 |
|
| |
| (6) |
We can define the crosscorrelation 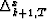 and the
reflection coefficient Kxp+1,T:
and the
reflection coefficient Kxp+1,T:
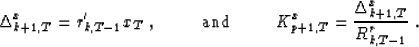
The time-updating is similar to equation (5). I use here an equation
derived from Lee et al. (1981), saying that for any vectors uT and
vT, we have the relationship:
| ![\begin{displaymath}
u'_T(P_{1,k,T}^{\perp}v_T)-u'_{T-1}(P_{1,k,T-1}^{\perp}v_{T-...
...\pi'_T(P_{1,k,T}^{\perp}v_T)].{1\over \cos^2\theta_{1,k,T}} \;.\end{displaymath}](img71.gif) |
(7) |
This equation, used with 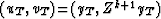 , leads
to the time-updating of
, leads
to the time-updating of 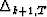 (equation (5)) in the
self-prediction of yT. Here, using the equation (8)
with uT=xT and vT=Zk+1yT, we get the time-update recursion:
(equation (5)) in the
self-prediction of yT. Here, using the equation (8)
with uT=xT and vT=Zk+1yT, we get the time-update recursion:
| 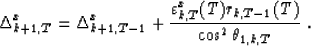 |
(8) |
The use of exponential tapering also gives a recursion similar to
equation (6):
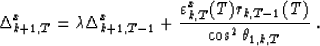
In conclusion, the recursions (7) and (9), joined
to the previous recursions (3), (4), and (5)
of the basic LSL algorithm, give us the entire set of recursions necessary
for the general LSL algorithm.





Next: Conclusion
Up: THE LSL ALGORITHM
Previous: Statistical signification of
Stanford Exploration Project
1/13/1998
![\begin{displaymath}
\sum_{t=0}^T (\varepsilon^x_{n,T}(t))^2 = \sum_{t=0}^T [x(t)-f_{n,T}(1)y(t-1)-\cdots-f_{n,T}(n)y(t-n)]^2\;.\end{displaymath}](img63.gif)
![\begin{displaymath}
\sum_{t=0}^T (\varepsilon^x_{n,T}(t))^2 = \sum_{t=0}^T [x(t)-f_{n,T}(1)y(t-1)-\cdots-f_{n,T}(n)y(t-n)]^2\;.\end{displaymath}](img63.gif)
![]() themselves, then
we have to find the orthogonal complement of xT
on the space
themselves, then
we have to find the orthogonal complement of xT
on the space ![]() . So, the idea is
to use the backward residuals of the self-prediction of yT
to form an orthogonal basis of the space Y1,k,T, and then
project the vector xT onto this particular basis.
Consequently, we will lead two recursions at the same time:
one to compute the variables
. So, the idea is
to use the backward residuals of the self-prediction of yT
to form an orthogonal basis of the space Y1,k,T, and then
project the vector xT onto this particular basis.
Consequently, we will lead two recursions at the same time:
one to compute the variables ![]() and rk,T of the
self-prediction of yT, and the other to compute the residuals
and rk,T of the
self-prediction of yT, and the other to compute the residuals
![]() of the joint prediction of xT from yT.
of the joint prediction of xT from yT.
![]() is very similar
to the updating of the residuals
is very similar
to the updating of the residuals ![]() . Effectively,
. Effectively,
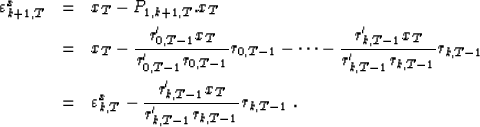
![]()
![]()