| |
(1) |
![]()
If we introduce a thin layer into the medium, the overall response of the reflected P wavefield beam (in the far-field approximation) at the surface, can be represented by the following expansion:
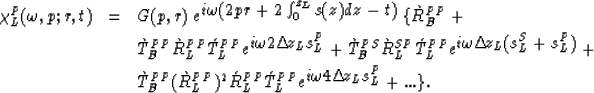 |
||
| (2) |
In the above equation, indexes P and S refer to P and S waves,
while indexes B and L correspond to the medium of
the incident wave (background or perturbation layer respectively).
R and T are the reflection and transmission coefficients,
while the accents (![]() and
and ![]() )
refer to the sense of propagation of
the incident wave. zL is the depth of
the top of the layer and
)
refer to the sense of propagation of
the incident wave. zL is the depth of
the top of the layer and ![]() its thickness. Finally,
sPL and sSL are the vertical slownesses of P and S waves
inside the layer. For instance,
its thickness. Finally,
sPL and sSL are the vertical slownesses of P and S waves
inside the layer. For instance, ![]() would
correspond to a P wave that is traveling upward inside the
layer and is reflected back at the top interface as an S wave.
would
correspond to a P wave that is traveling upward inside the
layer and is reflected back at the top interface as an S wave.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the rays corresponding to
the contributions of the two leading terms
of the expansion in equation (2); they represent
the P wave reflected by the top of the layer and the mode
that was transmitted to the layer, reflected in the bottom and
transmitted back again, always as a compressional wave.
shows the rays corresponding to
the contributions of the two leading terms
of the expansion in equation (2); they represent
the P wave reflected by the top of the layer and the mode
that was transmitted to the layer, reflected in the bottom and
transmitted back again, always as a compressional wave.
The first two terms of the expansion in equation (2) correspond to the two rays on the figure. The first is a P wave that is reflected as a P wave by the top of the layer, and the other corresponds to the same wave, transmitted into the layer as a P wave, reflect by the bottom still as P and then transmitted back to the background medium once again as a P wave.
Beneath the P wave's critical angle (and for geologically feasible elastic contrasts), the major contribution for the recorded P wave comes from the two first terms of the expansion in equation (2), and for angles close to the critical angle, the first-order conversion terms would be enough to suitably approximate the layer's reflection response. The approximation corresponding to the first two terms of the expansion is
| |
(3) |
![]()
If we add other thin layers into the model, the P wave response
of each layer can be expressed in the same way except for a multiplicative
factor, which accounts for the background transmission losses up to
that layer. It is important to emphasize that in
the same way as the perturbation
layer does not change traveltimes (which are kinematically-related),
nor does it influence average transmission losses
(because of the combined effect of all the overburden above any layer).
For this reason, I assume that the smoothly varying transmission
(and absorption) function
![]() must also be estimated by an independent method.
must also be estimated by an independent method.
The overall contribution from all layers is
| |
(4) |
Summing over time gives the
P wave impulsive-source response of the perturbed medium,
as the time Fourier-transform of ![]() :
:
| |
(5) |
For a given beam (p) the smooth background model can be used to find r(t), and the final result is achieved by summing the contributions from all beams. In my modeling program I used a superposition of one-half between adjacent beams and I smoothed around the central p of each beam with a triangle function.
A simple model (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) was used to
generate the synthetic data shown in Figure
) was used to
generate the synthetic data shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
It is important to notice that the seismic response from the
two adjacent perturbation layers does not correspond to
adjacent layers. The reason for this discrepancy is that the kinematics
inside the layer is different from the kinematics of
the background. To simulate the response of two
adjacent layers in the real world, the perturbation
model should have an overlap between layers (if the top layer
is faster than the background) or a gap between
them (top layer slower than background). On the other
hand, to transform the model space into the real world
model, a variable depth-shift (given by the difference
between the depth integrals of the background and perturbed model)
must be applied.
.
It is important to notice that the seismic response from the
two adjacent perturbation layers does not correspond to
adjacent layers. The reason for this discrepancy is that the kinematics
inside the layer is different from the kinematics of
the background. To simulate the response of two
adjacent layers in the real world, the perturbation
model should have an overlap between layers (if the top layer
is faster than the background) or a gap between
them (top layer slower than background). On the other
hand, to transform the model space into the real world
model, a variable depth-shift (given by the difference
between the depth integrals of the background and perturbed model)
must be applied.
Model used to generate the synthetic data in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The first 400 meters correspond
to water. The model is composed of a smoothly varying
background and some sparsely distributed layers.
. The first 400 meters correspond
to water. The model is composed of a smoothly varying
background and some sparsely distributed layers.
Synthetic data generated with the described method,
corresponding to the model of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
(a) p1/2 - t0 domain, and (b) x - t domain.
.
(a) p1/2 - t0 domain, and (b) x - t domain.