




Next: FORWARD MODELING
Up: Cunha: Elastic Inversion
Previous: Introduction
Before going ahead, it is important to answer the
following question: is the reflection response of
an interface separating two layers equivalent to the sum of
the responses of the two interfaces that separate each layer
from the background medium, as the separation between the
layers goes to zero?
This question is illustrated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The answer is yes, but only if we take into account all
the multiple conversions and internal reflections inside
the background sandwiched layer.
.
The answer is yes, but only if we take into account all
the multiple conversions and internal reflections inside
the background sandwiched layer.
I found however, after several numerical simulations (see
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), that
under some conditions (on the deviation of the perturbations
from the background) a good approximation can be achieved
by the consideration of only the primary P energy.
A theoretical consideration of this approximation is painful
for the elastic case, but its possible to have a good
feeling of the limitations involved by the analysis of
the simple case of normal incidence.
The reflection coefficient when the two layers are in
direct contact is
), that
under some conditions (on the deviation of the perturbations
from the background) a good approximation can be achieved
by the consideration of only the primary P energy.
A theoretical consideration of this approximation is painful
for the elastic case, but its possible to have a good
feeling of the limitations involved by the analysis of
the simple case of normal incidence.
The reflection coefficient when the two layers are in
direct contact is
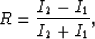
where Ix is the impedance of medium x (P velocity 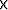 density).
density).
When the two layers are separated by the
background layer whose thickness approaches zero, the
reflection coefficient will be (if we consider only primaries)
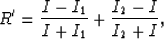
where I is the impedance of background medium.
This last expression can be put into the following form:
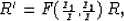
where
![\begin{displaymath}
F({\scriptstyle {I_1 \over I},{I_2 \over I}}) =
{2 \: [ {I_...
...I_2 \over I}]
\over [1 + {I_1 \over I}] [1 + {I_2 \over I}] }. \end{displaymath}](img5.gif)
The elastic response from an interface separating two layers
(I1 and I2) is modeled as the superposition
of the elastic responses from the two interfaces that separate
each layer from an hypothetical layer (I).
The ratio between modeled and actual normal incidence reflection
coefficient, as a function of the background impedance, for
fixed impedance between the two layers.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows how the ratio (F) between the
two reflection coefficients
behaves for fixed I1 and I2, and variable I. If the
impedance of the background medium lies between the impedance
of the two media, the ratio is very close to unity for any
practical case (for instance, Fmax= 1.03 for I2/I1=2).
shows how the ratio (F) between the
two reflection coefficients
behaves for fixed I1 and I2, and variable I. If the
impedance of the background medium lies between the impedance
of the two media, the ratio is very close to unity for any
practical case (for instance, Fmax= 1.03 for I2/I1=2).
The differences between the reflectivities for non-normal
incidence were computed for some specific cases corresponding
to a background P velocity of 2500 m/s and a maximum variation
of 500 m/s around it for the perturbation layers. The results
are shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . All graphs start at p1/2=0.012
(which corresponds to an angle of 21 degrees in the background
layer) because the errors are too small for smaller values. For
figures (a), (b), (e) and (f) (in which
the velocity of the slowest medium (1) is held constant), the error
starts to grow near the critical angle of medium 2 (when its
velocity is larger than the background) or near the critical
angle of the background (when medium 2 is slower than the
background). On the other hand, when the velocity of the
fastest medium (2) is fixed (figures (c), (d), (g)
and (h)), the error begins to increase near the critical
angle of medium 2. We conclude then that the approximation
is valid, up to the critical angle of the faster of the
three media involved.
. All graphs start at p1/2=0.012
(which corresponds to an angle of 21 degrees in the background
layer) because the errors are too small for smaller values. For
figures (a), (b), (e) and (f) (in which
the velocity of the slowest medium (1) is held constant), the error
starts to grow near the critical angle of medium 2 (when its
velocity is larger than the background) or near the critical
angle of the background (when medium 2 is slower than the
background). On the other hand, when the velocity of the
fastest medium (2) is fixed (figures (c), (d), (g)
and (h)), the error begins to increase near the critical
angle of medium 2. We conclude then that the approximation
is valid, up to the critical angle of the faster of the
three media involved.
All figures correspond to vmin=2000m/s, vmax=3000m/s,
vback=2500m/s, 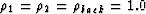 g/cc (v refers to
P velocities,
g/cc (v refers to
P velocities, 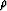 to density, and indexes 1, 2 and back,
to media 1, 2 and background respectively). Different curves
correspond to increasing P velocity of medium 1 or 2, according
to the following convention: continuous=2167, dot=2333,
dot-dash=2500, fine-dash=2667, large-dash=2833. (a)
to density, and indexes 1, 2 and back,
to media 1, 2 and background respectively). Different curves
correspond to increasing P velocity of medium 1 or 2, according
to the following convention: continuous=2167, dot=2333,
dot-dash=2500, fine-dash=2667, large-dash=2833. (a)
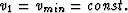 ,
, 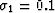 ,
, 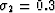 ,
,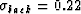 (
( represents Poisson's ratios), and
v2 has a different value for each curve (according to previous
convention). (b) Same as a, except that
represents Poisson's ratios), and
v2 has a different value for each curve (according to previous
convention). (b) Same as a, except that
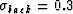 . (c) Same as a, except that
. (c) Same as a, except that
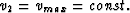 and v1 varying.
(d) Same as c, except that
and v1 varying.
(d) Same as c, except that 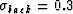 .
(e), (f), (g), and (h), are equivalent
to the previous four, with the only difference of
.
(e), (f), (g), and (h), are equivalent
to the previous four, with the only difference of
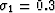 ,
, 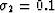 .
.





Next: FORWARD MODELING
Up: Cunha: Elastic Inversion
Previous: Introduction
Stanford Exploration Project
1/13/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), that
under some conditions (on the deviation of the perturbations
from the background) a good approximation can be achieved
by the consideration of only the primary P energy.
A theoretical consideration of this approximation is painful
for the elastic case, but its possible to have a good
feeling of the limitations involved by the analysis of
the simple case of normal incidence.
The reflection coefficient when the two layers are in
direct contact is
), that
under some conditions (on the deviation of the perturbations
from the background) a good approximation can be achieved
by the consideration of only the primary P energy.
A theoretical consideration of this approximation is painful
for the elastic case, but its possible to have a good
feeling of the limitations involved by the analysis of
the simple case of normal incidence.
The reflection coefficient when the two layers are in
direct contact is
![\begin{displaymath}
F({\scriptstyle {I_1 \over I},{I_2 \over I}}) =
{2 \: [ {I_...
...I_2 \over I}]
\over [1 + {I_1 \over I}] [1 + {I_2 \over I}] }. \end{displaymath}](img5.gif)