




Next: About this document ...
Up: Cunha: Beam stack
Previous: REFERENCES
If we disregard absorption and transmission losses, and
consider the asymptotic approximation (where the ray
theory holds), the integral of the energy flux over a
wavefront inside a Snell beam, is a constant of propagation.
This condition can be expressed by
| 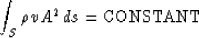 |
(2) |
(Aki and Richards, 1980), where S is the wavefront surface,
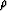 is the density of the medium, and v and A are the
velocity and amplitude of the wave.
equation (2) applies to both the
downward and upward ring-shaped propagating wavefront
of Figure
is the density of the medium, and v and A are the
velocity and amplitude of the wave.
equation (2) applies to both the
downward and upward ring-shaped propagating wavefront
of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , but the constants are different
before and after the reflection.
, but the constants are different
before and after the reflection.
An azimuthly symmetric conical beam is reflected by an
interface. Under the assumption of a plane-layered earth,
the amplitude at any point of the ring-shaped wavefront
depends only on the Snell parameter p and the offset x.
Let's first apply equation (2) for the downgoing beam,
at a unit distance from the source, and just before it hits the
reflector:
| 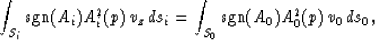 |
(3) |
where the indexes and i apply to the wavefronts near the source
and near the reflector, respectively.
The sgn function introduced in equation (3) does
not affect the equality. It is possible to integrate separately
infinitesimal beams with positive and negative amplitudes, and the equality
will still hold for both independently, since no sign change is possible
inside a beam.
Applying equation (2) for the upcoming beam; just after the
reflection and just before it hits the surface, we find that
| 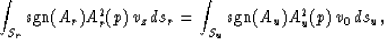 |
(4) |
where the indexes r and u apply for the wavefronts near the reflector
and near the surface, respectively.
I define now an average amplitude square over a wavefront, in
such a way that it keeps the ``average sign of the wavefront"
| 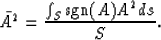 |
(5) |
It is possible then to have an estimation of the average
reflection coefficient over the region illuminated by the
beam through the following relation
| 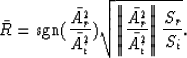 |
(6) |
Dividing equation (4) by equation (3) and
using equations (6) and (5) results in
| 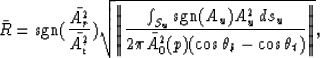 |
(7) |
where 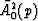 is an average (in the sense of equation (5))
estimation of the source radiation pattern, for the beam with
Snell parameter p, at unit distance from the source.
Indexes b and t apply for the
bottom and top rays of the beam as illustrated in Figure
is an average (in the sense of equation (5))
estimation of the source radiation pattern, for the beam with
Snell parameter p, at unit distance from the source.
Indexes b and t apply for the
bottom and top rays of the beam as illustrated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
Vertical cross section of the upcoming beam. If we
approximate the surface S by a conical surface, the
area element ds is given by 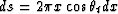 .
.
A last necessary assumption is that
| 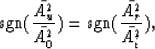 |
(8) |
which is equivalent to the assumption that the signal of the average
described by equation (5) does not change during
propagation, unless the beam is reflected.
Finally, if the wavefront ring reaching the surface is approximated
by a conical surface, the application of straightforward geometry
leads to
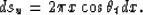
Using this result and substituting equation (8) into
equation (7), a final expression for the output sample
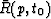 is found:
is found:
| ![\begin{displaymath}
\bar{R}(p,t_0) = H(p_t,p_b,t_0) \mbox{sgn}(\bar{A^2_u})
\sqr...
...nt_{x_b}^{x_t} \mbox{sgn}(A_u) A^2_u(x,t[x,t_0]) x dx } \Vert},\end{displaymath}](img16.gif) |
(9) |
where
| 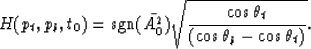 |
(10) |
All the cosine factors in equation (10) can be expressed in terms of
pt or pb, the horizontal slownesses of the boundary
rays of the beam, according to
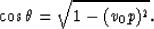
The offsets xt and xb that appear
in the integral limits of equation (9) are determined by
the interceptions (in the x-t domain) of the top and bottom
rays with the reflection curve (or wavefront) t=t(x,t0).
The specific function that
describes the wavefronts in the x-t domain
can be given either explicitly by
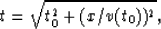
if an hyperbolic approximation is satisfactory,
or implicitly with the use of raytracing.





Next: About this document ...
Up: Cunha: Beam stack
Previous: REFERENCES
Stanford Exploration Project
1/13/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , but the constants are different
before and after the reflection.
, but the constants are different
before and after the reflection.
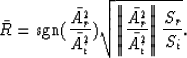
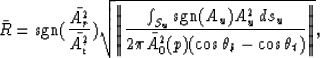
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
![]() .
.![]()
![]()
![]()