DEFINING THE TRANSFORM

The proposed transform is a variation of the slant-stack, that mixes concepts of beam-stack and Snell rays. Beam-stacks can be used to achieve a better resolution in the computation of slant-stack, as described by Kostov and Biondi (1987). Basically, beam-stacks perform a local sum over hyperbolic trajectories (in the x-t domain), which are parametrized by the vertical traveltime, offset, and horizontal slowness. Therefore, although the transformed domain is one dimension higher than the original, the method has the advantage that no apriori velocity model is required.

I define the transform so that, under some usual assumptions, the transformed data would provide an averaged, relative amplitude response of the subsurface region illuminated by a Snell beam. The assumptions are, that within the range of a CMP gather the subsurface geology can be approximated by a plane-layered, isotropic elastic medium; that a previous multiple-removal process had been applied; and that transmission losses are either negligible or previously corrected. However, only the first assumption is required for the validity of the transform, which properly compensates for the effects of spherical divergence, source and receiver radiation patterns and normal-moveout.

Figure  shows two Snell beams illuminating a small subsurface region. Each beam is defined by the Snell parameters (horizontal slowness) of the boundary rays of the beam, and if we do not take into account transmission or absorption losses, the total energy in a wavefront inside the beam remains constant before and after the reflection. Therefore, the ratio between the energy in a wavefront recorded at the surface and the energy in a wavefront near the source will be affected only by the reflection losses.

A small region of a reflector is illuminated by two Snell beams.

The transformation is performed in the following way:

• Using an a priori velocity model, we first define a given number of Snell rays in a common midpoint gather. Thus, within the limits of ray theory, the energy propagating between any two adjacent rays (which I will term a Snell beam) is constant at any wavefront.
• Then, using the same velocity model, we define for each vertical traveltime (t₀), those curves in the x-t domain that correspond to the reflected wavefronts. This stage can be accomplished either by a usual hyperbolic fit, or by raytracing (which, of course, substantially slows down the process).
• Finally, for each vertical travel time (t₀) and each beam, we perform a weighted sum of the amplitude squared, of the samples inside the beam, along the curve corresponding to that particular t₀. This sum will generate a sample in the transformed space, at time t₀ and Snell parameter given by the central horizontal slowness of the beam.

The analytic expression for the described transform is  

$$\bar{R}(p,t_0) = H(p_t,p_b,t_0) \, \mbox{sgn}(\bar{A^2_u}) \... ...int_{S_u} \mbox{sgn}(A_u) A^2_u(x,t[x,t_0])\, x \, dx } \Vert},$$ (1)

where x is the shot-receiver offset; A_u is the amplitude of the recorded upcoming field at offset x and time t; x_t (x_b) is the offset corresponding to the crossing point between the top (bottom) ray of the beam and the reflection curve associated with time t₀; and H is a factor that depends on t₀ and the horizontal slownesses p_t and t_b of the top and bottom rays of the beam. The exact expression for H, as well as the derivation of equation (1) and the exact meaning of 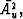$\bar{A^2_u},$ are given in Appendix A.

I have tested two possibilities for the sampling rate of the horizontal slowness (i.e. the interval between adjacent output traces). In one case, the Snell parameter interval was kept constant, and in the other the interval between the square roots of two adjacent Snell parameters was fixed. I prefer this second option, because the transformed data shows a more uniform scanning of the x-t domain (Figure ).

Snell beams corresponding to (a) a constant interval between adjacent values of the square root of p, and (b) a constant interval between adjacent values of p.

For shallow reflectors and large values of horizontal slowness, the hyperbolic approximation for the reflected wavefront loses its validity and a ray-tracing routine (controlled by the background model) must be used to determine the stacking curve.

The main advantages of this transformation are that no further moveout correction is required; geometrical spreading correction is done in an appropriate way; the effects of source directivity are directly incorporated in the transform; the transformed dataset approximates a local plane-wave response at the reflector's position; the number of undesirable events that are summed to the signal is considerably smaller here than in the conventional slant-stack, since just a local sum is involved. Although the method described uses an apriori velocity model, a data-driven Snell ray-tracing can be implemented as described by Ottolini (1987) or using of a local dip estimation process (Claerbout, 1990).