




Next: APPENDIX C
Up: Jedlicka: Velocity analysis by
Previous: APPENDIX B
The aim of this section is to derive the expression for the operator
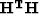 .We know that
.We know that
| 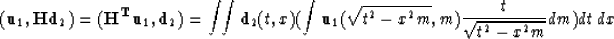 |
(36) |
for any  from
from  -space and
-space and 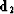 from
(t,x)-space.
If we define
from
(t,x)-space.
If we define
| 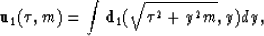 |
(37) |
then
| 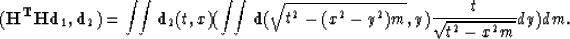 |
(38) |
From this equation it follows
| 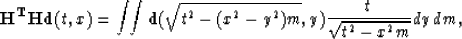 |
(39) |
which is the expression for the operator 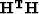 .
.
Equation 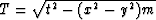 represents a
hyperbola in (T,y)-space passing through the point (t,x).
With changing m we obtain a set of hyperbolas passing through the
point (t,x) (Fig
represents a
hyperbola in (T,y)-space passing through the point (t,x).
With changing m we obtain a set of hyperbolas passing through the
point (t,x) (Fig ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). A weighting factor is assigned
to each hyperbola. The higher the slope of a hyperbola is, the
higher weighting factor is assigned.
The value of the operator
). A weighting factor is assigned
to each hyperbola. The higher the slope of a hyperbola is, the
higher weighting factor is assigned.
The value of the operator 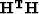 at the point (t,x) is equal
to the weighted sum of all values lying on the hyperbolas passing
through the point (t,x).
at the point (t,x) is equal
to the weighted sum of all values lying on the hyperbolas passing
through the point (t,x).
This result may also be explained in the following way.
The sums along hyperbolas passing through the point (t,x)
form a parabola in 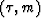 -space (Jedlicka, 1989).
-space (Jedlicka, 1989).
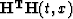 is obtained by weighted summation along this parabola.
Each point of the parabola represents a sum along a corresponding
hyperbola, from which the previous result follows immediately.
is obtained by weighted summation along this parabola.
Each point of the parabola represents a sum along a corresponding
hyperbola, from which the previous result follows immediately.
If d(t,x)=1 for all t and x then from equation (39)
it follows
| 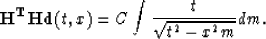 |
(40) |
This means that count(t,x) for velocity analysis is equal to the
sum of NMO counts over the range of velocities used in velocity analysis.
An expression for a count for NMO is derived in Appendix C.





Next: APPENDIX C
Up: Jedlicka: Velocity analysis by
Previous: APPENDIX B
Stanford Exploration Project
1/13/1998
![]() represents a
hyperbola in (T,y)-space passing through the point (t,x).
With changing m we obtain a set of hyperbolas passing through the
point (t,x) (Fig
represents a
hyperbola in (T,y)-space passing through the point (t,x).
With changing m we obtain a set of hyperbolas passing through the
point (t,x) (Fig ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). A weighting factor is assigned
to each hyperbola. The higher the slope of a hyperbola is, the
higher weighting factor is assigned.
The value of the operator
). A weighting factor is assigned
to each hyperbola. The higher the slope of a hyperbola is, the
higher weighting factor is assigned.
The value of the operator ![]() at the point (t,x) is equal
to the weighted sum of all values lying on the hyperbolas passing
through the point (t,x).
at the point (t,x) is equal
to the weighted sum of all values lying on the hyperbolas passing
through the point (t,x).
![]() -space (Jedlicka, 1989).
-space (Jedlicka, 1989).
![]() is obtained by weighted summation along this parabola.
Each point of the parabola represents a sum along a corresponding
hyperbola, from which the previous result follows immediately.
is obtained by weighted summation along this parabola.
Each point of the parabola represents a sum along a corresponding
hyperbola, from which the previous result follows immediately.