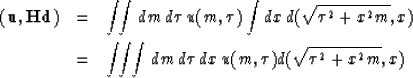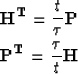Next: APPENDIX B
Up: Jedlicka: Velocity analysis by
Previous: APPENDIX A
A natural extension of dot products in (t,x)-space and 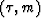 -space
in a continuous domain is
-space
in a continuous domain is
| 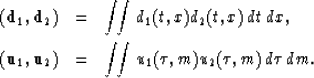 |
(22) |
| (23) |
The definition of an adjoint operator in a continuous domain cannot be done
straightforwardly by transposing a corresponding matrix (we simply do not have
the matrix). Instead another
equivalent property is used for definition:
| 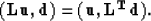 |
(24) |
This is the equation that is used for the dot product tests (Claerbout, 1985).
The definition of a velocity stacking operator 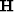 in (t,x)-space is
in (t,x)-space is
| 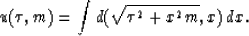 |
(25) |
Similarly we can define a stacking operator 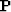 in
in 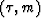 -space:
-space:
| 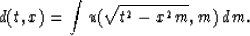 |
(26) |
Now the question is what is the relationship between the two operators.
It can be shown (Thorson, 1984) that they are adjoint for dot products
defined by equations
| 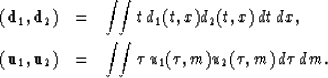 |
(27) |
| (28) |
They are not, however, adjoint for the dot products defined by equations (23).
If we want to apply an algorithm using Euclidean norms, then our operators
should be adjoint with respect to the Euclidean norms.
Let us derive the adjoint operator 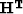 :
:
| 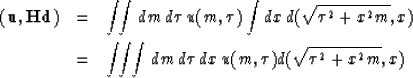 |
(29) |
| (30) |
After substitution 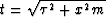 ,
, 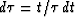 we obtain
we obtain
| 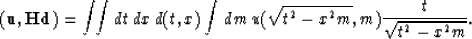 |
(31) |
Finally we have
| 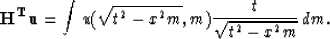 |
(32) |
Similarly the adjoint operator 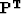 may be derived:
may be derived:
| 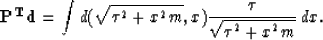 |
(33) |
For short reference we will write the above equations symbolically
| 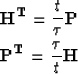 |
(34) |
| (35) |
We may weight both operators in the offset and velocity space.
Here an infinite number of weighting factors can be obtained and a problem
is which pair of them to choose. Here are some of them:





Next: APPENDIX B
Up: Jedlicka: Velocity analysis by
Previous: APPENDIX A
Stanford Exploration Project
1/13/1998
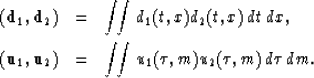
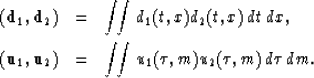
![]() in (t,x)-space is
in (t,x)-space is
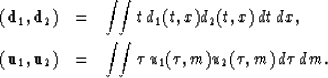
![]() :
: