




Next: VELOCITY ANALYSIS
Up: Jedlicka: Velocity analysis by
Previous: Introduction
Let us denote 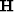 as the operator of summation along hyperbolas.
The operator
as the operator of summation along hyperbolas.
The operator 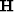 transforms (t,x)-space into
transforms (t,x)-space into 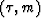 -space:
-space:
| 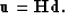 |
(2) |
An adjoint operator 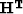 transforms
transforms 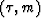 -space into
(t,x)-space:
-space into
(t,x)-space:
| 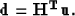 |
(3) |
We can also define a stacking operator in 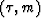 -space. Because
-space. Because
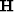 maps a point onto a parabola (Jedlicka, 1989b), it is natural
to define an operator
maps a point onto a parabola (Jedlicka, 1989b), it is natural
to define an operator 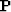 as an operator of summation along parabolas:
as an operator of summation along parabolas:
| 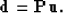 |
(4) |
The adjoint operator 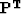 ,
,
| 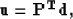 |
(5) |
may serve as an alternative operator for velocity analysis.
Here each point in (t,x)-space is spread onto a parabola
in 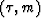 -space.
Both operators
-space.
Both operators 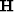 and
and 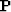 are linear.
The relationship between them is shown in Appendix A.
are linear.
The relationship between them is shown in Appendix A.





Next: VELOCITY ANALYSIS
Up: Jedlicka: Velocity analysis by
Previous: Introduction
Stanford Exploration Project
1/13/1998