




Next: Examples of matrices
Up: SAMPLING IN VELOCITY DOMAIN
Previous: SAMPLING IN VELOCITY DOMAIN
Stacking along hyperbolas is a linear operator mapping a two-dimensional
(t,x)-space into two-dimensional 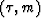 -space. The operator may
therefore be expressed as a matrix in a four-dimensional space.
This is not
convenient for our imagination. The representation of the operator
in two dimensions is preferable. This can be achieved by ordering all
the columns of (t,x)-space into one vector, and the same for
-space. The operator may
therefore be expressed as a matrix in a four-dimensional space.
This is not
convenient for our imagination. The representation of the operator
in two dimensions is preferable. This can be achieved by ordering all
the columns of (t,x)-space into one vector, and the same for 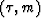 -space.
To get an idea of what the matrix looks like, let us write the equation
transforming (t,x)-space into
-space.
To get an idea of what the matrix looks like, let us write the equation
transforming (t,x)-space into 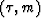 -space
when the number of samples is six, two offsets and two sloths.
The nearest neighbor interpolation was used.
-space
when the number of samples is six, two offsets and two sloths.
The nearest neighbor interpolation was used.
|  |
(14) |
Each submatrix in the matrix represents 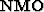 transformation (Claerbout,
1989). The transpose matrix applied on u gives d:
transformation (Claerbout,
1989). The transpose matrix applied on u gives d:
|  |
(15) |
Generally, if we denote 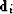 as the i-th trace of a gather,
as the i-th trace of a gather, 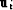 as the
i-th trace of a velocity analysis panel and
as the
i-th trace of a velocity analysis panel and 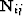 as an NMO matrix
transforming i-th offset with j-th sloth, then the velocity stacking
transformation may be expressed by the equation
as an NMO matrix
transforming i-th offset with j-th sloth, then the velocity stacking
transformation may be expressed by the equation
|  |
(16) |
If we want to compute 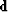 from
from  by least squares,
then the matrix
by least squares,
then the matrix 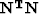
| 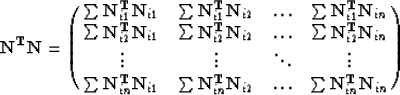 |
(17) |
should be inverted. This matrix is not even approximately unitary, as it
is for 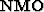 (Claerbout, 1989). For our example we have
(Claerbout, 1989). For our example we have
|  |
(18) |
Hence just a transpose operation to stacking cannot be used for inverting
the velocity analysis panel.
The rank of the matrix 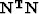 cannot be higher than max(n.nt,k.nt),
where nt is the number of samples of a trace.
From this it follows that the matrix
cannot be higher than max(n.nt,k.nt),
where nt is the number of samples of a trace.
From this it follows that the matrix 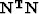 is singular if the number of traces in the
is singular if the number of traces in the 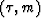 -space
is less than the number of traces in (t,x)-space.
Generally, this matrix may be expected to be singular even for the opposite case,
as we can see from equation (18).
-space
is less than the number of traces in (t,x)-space.
Generally, this matrix may be expected to be singular even for the opposite case,
as we can see from equation (18).





Next: Examples of matrices
Up: SAMPLING IN VELOCITY DOMAIN
Previous: SAMPLING IN VELOCITY DOMAIN
Stanford Exploration Project
1/13/1998


![]() transformation (Claerbout,
1989). The transpose matrix applied on u gives d:
transformation (Claerbout,
1989). The transpose matrix applied on u gives d:


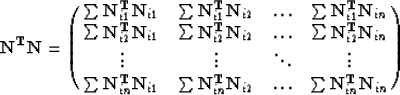

![]() cannot be higher than max(n.nt,k.nt),
where nt is the number of samples of a trace.
From this it follows that the matrix
cannot be higher than max(n.nt,k.nt),
where nt is the number of samples of a trace.
From this it follows that the matrix ![]() is singular if the number of traces in the
is singular if the number of traces in the ![]() -space
is less than the number of traces in (t,x)-space.
Generally, this matrix may be expected to be singular even for the opposite case,
as we can see from equation (18).
-space
is less than the number of traces in (t,x)-space.
Generally, this matrix may be expected to be singular even for the opposite case,
as we can see from equation (18).