




Next: RATE OF CONVERGENCE
Up: Jedlicka: Cascaded normal moveout
Previous: PARTIAL NORMAL MOVEOUT
Let us write
| 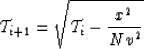 |
(15) |
for the nontruncated case and
| 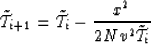 |
(16) |
for the truncated case.
We will estimate the difference 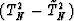 and show that this difference tends to zero as
and show that this difference tends to zero as 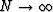 .We can write
.We can write
| 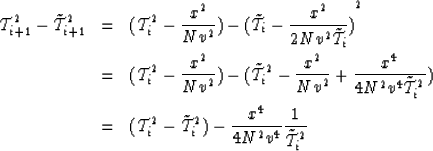 |
(17) |
| (18) |
| (19) |
As we did in the previous section, we can rewrite this equation into a
system of equations:
| 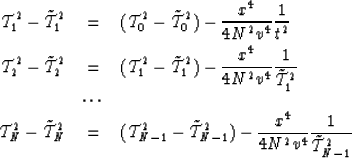 |
(20) |
| (21) |
| (22) |
| (23) |
By summing up all these equations we get
| 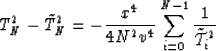 |
(24) |
Now we need to prove that there exists a constant K independent of N such that
| 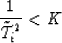 |
(25) |
for all 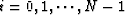 .From equation (16) we can see that
.From equation (16) we can see that
| 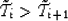 |
(26) |
Similarly from equation (24) we can see that
| 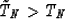 |
(27) |
Putting both equations together we have
| 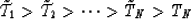 |
(28) |
or
| 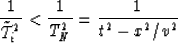 |
(29) |
where the last equation follows from equation (14).
If we define
| 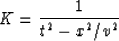 |
(30) |
then from equation (24) we have
| 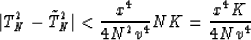 |
(31) |
which tends to zero as 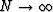 .This proves that the Nth partial normal moveout applied N times is equal
to the normal moveout for large N.
.This proves that the Nth partial normal moveout applied N times is equal
to the normal moveout for large N.
The convergence of cascaded NMO to a semicircle can be clearly seen
on Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a. The proof of convergence holds for
a. The proof of convergence holds for 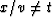 .
The behavior for x/v = t can be seen from sequences at the sides of
Figure
.
The behavior for x/v = t can be seen from sequences at the sides of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b. The figure convinces us that there is convergence even
for x/v=t, but that it is extremely slow.
b. The figure convinces us that there is convergence even
for x/v=t, but that it is extremely slow.





Next: RATE OF CONVERGENCE
Up: Jedlicka: Cascaded normal moveout
Previous: PARTIAL NORMAL MOVEOUT
Stanford Exploration Project
1/13/1998
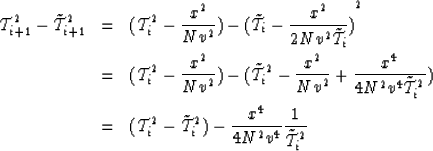
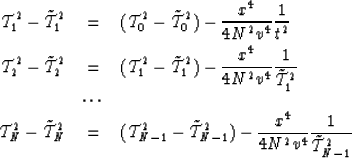
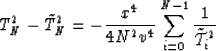
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a. The proof of convergence holds for
a. The proof of convergence holds for ![]() .
The behavior for x/v = t can be seen from sequences at the sides of
Figure
.
The behavior for x/v = t can be seen from sequences at the sides of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b. The figure convinces us that there is convergence even
for x/v=t, but that it is extremely slow.
b. The figure convinces us that there is convergence even
for x/v=t, but that it is extremely slow.