




Next: Structural analysis
Up: VELOCITY INFORMATION FROM MIGRATED
Previous: VELOCITY INFORMATION FROM MIGRATED
In SEP-60 I discussed an optimization method that backprojects perturbations
in prestack migrated events onto the velocity model.
In general, the perturbations are not readily available; picking them
on the constant surface location gathers is cumbersome and not very
reliable for the data shown here.
However, it may be feasible to pick events from the migrated
constant-offset sections after they have been locally stacked to
reduce noise. The sections resemble the geology, at least for the inner
offsets, as can be seen in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
A method that avoids picking altogether uses semblance derivatives,
and was described in my previous report. Semblance in the
stacked image is calculated
along stacking trajectories in the prestack migrated data. Instead
of picking perturbations in the stacking trajectory, semblance
derivatives along the trajectory drive the optimization method.
I briefly review the calculations here; for more details I refer the reader to
the SEP-60.
The derivative of semblance J with respect to zm for a certain event
is:
| 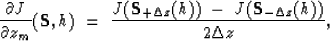 |
(1) |
where h is offset, and (xm,zm)
the position after migration.
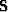 is the current stacking trajectory, and
is the current stacking trajectory, and 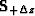 and
and 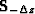 are
perturbations thereof.
are
perturbations thereof. 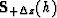 is the upward perturbed trajectory;
it is the same as
is the upward perturbed trajectory;
it is the same as  , except
for a perturbation by
, except
for a perturbation by 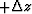 in the zm direction
at offset h:
in the zm direction
at offset h:
| 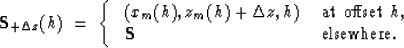 |
(2) |
Likewise, 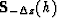 is perturbed by
is perturbed by 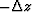 at offset h.
at offset h.
The gradient calculation is not very robust if the trajectory is just shifted at
one offset, as described in the above equation.
Therefore, the path is perturbed at several offsets,
with the perturbations decreasing away from the offset under consideration.
This is schematically illustrated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.





Next: Structural analysis
Up: VELOCITY INFORMATION FROM MIGRATED
Previous: VELOCITY INFORMATION FROM MIGRATED
Stanford Exploration Project
1/13/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.