




Next: Predictive deconvolution
Up: SYNTHETIC EXAMPLE
Previous: SYNTHETIC EXAMPLE
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the results of the L2 and L1 deconvolutions for
the pure trace. Because the original wavelet lacked very low and very high
frequencies, I used a damping factor for both deconvolutions: 1/1000 of the
autocorrelation
shows the results of the L2 and L1 deconvolutions for
the pure trace. Because the original wavelet lacked very low and very high
frequencies, I used a damping factor for both deconvolutions: 1/1000 of the
autocorrelation 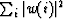 in the L2 algorithm, and 1/1000 of the
weighted autocorrelation
in the L2 algorithm, and 1/1000 of the
weighted autocorrelation 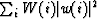 at each iteration of the L1
algorithm. The results are similar, as no noise was introduced. The ringing
around the main peaks comes from the lack of high frequencies in the data,
which forces the output to be convolved with a ``sinc'' function (impulse
response of a high-cut filter).
at each iteration of the L1
algorithm. The results are similar, as no noise was introduced. The ringing
around the main peaks comes from the lack of high frequencies in the data,
which forces the output to be convolved with a ``sinc'' function (impulse
response of a high-cut filter).
Then I did the same process with the noisy trace. The results are presented
on Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Even with a damping factor, the L2 deconvolution
cannot avoid the influence of the noise, because a damping factor is adapted
to gaussian noise. By giving the same weights to all the residuals (W=Identity
matrix), it overestimates the importance of the noise bursts, and damages
the output around these bursts. On the contrary, as expected, the L1
deconvolution is insensitive to this noise.
. Even with a damping factor, the L2 deconvolution
cannot avoid the influence of the noise, because a damping factor is adapted
to gaussian noise. By giving the same weights to all the residuals (W=Identity
matrix), it overestimates the importance of the noise bursts, and damages
the output around these bursts. On the contrary, as expected, the L1
deconvolution is insensitive to this noise.





Next: Predictive deconvolution
Up: SYNTHETIC EXAMPLE
Previous: SYNTHETIC EXAMPLE
Stanford Exploration Project
1/13/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Even with a damping factor, the L2 deconvolution
cannot avoid the influence of the noise, because a damping factor is adapted
to gaussian noise. By giving the same weights to all the residuals (W=Identity
matrix), it overestimates the importance of the noise bursts, and damages
the output around these bursts. On the contrary, as expected, the L1
deconvolution is insensitive to this noise.
. Even with a damping factor, the L2 deconvolution
cannot avoid the influence of the noise, because a damping factor is adapted
to gaussian noise. By giving the same weights to all the residuals (W=Identity
matrix), it overestimates the importance of the noise bursts, and damages
the output around these bursts. On the contrary, as expected, the L1
deconvolution is insensitive to this noise.