 |
 |
 |
 | Subsalt imaging by target-oriented wavefield least-squares migration: A 3-D field-data example |  |
![[pdf]](icons/pdf.png) |
Next: 3-D field-data examples
Up: theory
Previous: The 3-D phase-encoded Hessian
Regularization helps to stabilize the inversion; it can shape the null space and remove unwanted features in the inverted result by introducing
user-defined model-covariance operators. In this paper, we choose to use the following regularization term:
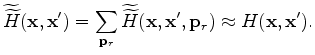 |
|
|
(13) |
where operator 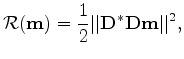 contains wavekill filters (Claerbout, 2008), which annihilate local planar-events with given dips.
The operator imposes continuity of reflectors along its dipping direction.
This idea has also been explored by Clapp (2005) and Ayeni et al. (2009), who use similar filters (Hale, 2007; Clapp, 2003) to regularize
the data-domain least-squares migration.
contains wavekill filters (Claerbout, 2008), which annihilate local planar-events with given dips.
The operator imposes continuity of reflectors along its dipping direction.
This idea has also been explored by Clapp (2005) and Ayeni et al. (2009), who use similar filters (Hale, 2007; Clapp, 2003) to regularize
the data-domain least-squares migration.
Instead of solving the inversion problem as a regularization problem, we solve it as a preconditioning
problem by making change of variables as follows:
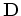 |
|
|
(14) |
where 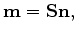 is the vector of preconditioned variables and
is the vector of preconditioned variables and 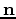 is the preconditioning operator, which
is defined to be an approximate inverse of the regularization operator
is the preconditioning operator, which
is defined to be an approximate inverse of the regularization operator
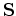 .
To find the inverse of
.
To find the inverse of
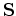 , we factorize it into minimum-phase filters
, we factorize it into minimum-phase filters 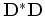 such that
such that
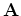 . We use the Wilson-Burg factorization (Fomel et al., 2003; Claerbout, 1992)
and apply it on the helix (Claerbout, 2008,1998). Since minimum-phase filters have stable inverses, we can define
the preconditioning operator as follows:
. We use the Wilson-Burg factorization (Fomel et al., 2003; Claerbout, 1992)
and apply it on the helix (Claerbout, 2008,1998). Since minimum-phase filters have stable inverses, we can define
the preconditioning operator as follows:
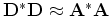 |
|
|
(15) |
Unlike
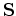 , operator
, operator 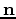 contains dip filters, which smooth along given dip directions.
Substituting equations 13, 14 and 15
into 1 yields
contains dip filters, which smooth along given dip directions.
Substituting equations 13, 14 and 15
into 1 yields
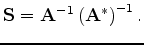 |
|
|
(16) |
Objective function 16 is often solved by setting 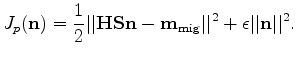 and iterating until
an acceptable result is obtained (Claerbout, 2008). Solving it in this way implicitly assumes that we are starting with
a model that has all the user-defined covariance, and that the more iterations we run, the more
we honor the data. Once a solution vector
and iterating until
an acceptable result is obtained (Claerbout, 2008). Solving it in this way implicitly assumes that we are starting with
a model that has all the user-defined covariance, and that the more iterations we run, the more
we honor the data. Once a solution vector
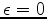 has been found, the final
model is obtained by computing
has been found, the final
model is obtained by computing
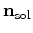 .
.
 |
 |
 |
 | Subsalt imaging by target-oriented wavefield least-squares migration: A 3-D field-data example |  |
![[pdf]](icons/pdf.png) |
Next: 3-D field-data examples
Up: theory
Previous: The 3-D phase-encoded Hessian
2011-05-24
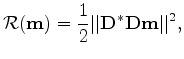 contains wavekill filters (Claerbout, 2008), which annihilate local planar-events with given dips.
The operator imposes continuity of reflectors along its dipping direction.
This idea has also been explored by Clapp (2005) and Ayeni et al. (2009), who use similar filters (Hale, 2007; Clapp, 2003) to regularize
the data-domain least-squares migration.
contains wavekill filters (Claerbout, 2008), which annihilate local planar-events with given dips.
The operator imposes continuity of reflectors along its dipping direction.
This idea has also been explored by Clapp (2005) and Ayeni et al. (2009), who use similar filters (Hale, 2007; Clapp, 2003) to regularize
the data-domain least-squares migration.
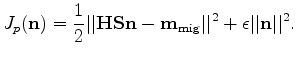 and iterating until
an acceptable result is obtained (Claerbout, 2008). Solving it in this way implicitly assumes that we are starting with
a model that has all the user-defined covariance, and that the more iterations we run, the more
we honor the data. Once a solution vector
and iterating until
an acceptable result is obtained (Claerbout, 2008). Solving it in this way implicitly assumes that we are starting with
a model that has all the user-defined covariance, and that the more iterations we run, the more
we honor the data. Once a solution vector