A log spectral approach to bidirectional deconvolution

THE LOG SPECTRAL APPROACH

A minimum phase wavelet can be made from any causal wavelet by taking it to Fourier space, and exponentiating. The proof is straightforward: Let $U(Z)= 1 + u_1 Z + u_2 Z^2 +\cdots$ be the $Z$ transform ( $Z=e^{i\omega}$ ) of any causal function. Then $e^{U(Z)}$ will be minimum phase. Although we would always do this calculation in the Fourier domain, the easy proof is in the time domain. The power series for an exponential $e^U= 1 + U + U^2/2! + U^3/3! +\cdots$ has no powers of $1/Z$ , and it always converges because of the powerful influence of the denominator factorials. Likewise $e^{-U}$ , the inverse of $e^U$ , always converges and is causal. Thus both the filter and its inverse are causal. Q.E.D.

We seek to find two functions, one strictly causal the other strictly anticausal (nothing at $t=0$ ).

$$U^+ = u_1 Z + u_2 Z^2+ \cdots$$ (1)

$$U^- = u_{-1}/Z + u_{-2}/Z^2+ \cdots$$ (2)

Notice $U$ , $U^2$ , etc do not contain $Z^0$ . Thus the coefficient of $Z^0$ in $e^U=1+U+U^2/2!+\cdots$ is unity. Thus $a_0=b_0=1$ .

$$e^{U^+} \ =\ A = 1 + a_1 Z + a_2 Z^2 + \cdots$$ (3)

$$e^{U^-} \ =\ B = 1 + b_1 /Z + b_2 /Z^2 + \cdots$$ (4)

Define $U = U^- + U^+$ . The decon filter is $AB=e^U$ and the source waveform is its inverse $e^{-U}$ . With the Fourier transform of the data $D(\omega)$ , the decon output is:

$$\mathbf{r} = (r_t) = {\rm FT}^{-1} \ D(\omega)\ e^{U(Z(\omega))}$$ (5)

where $U$ is found with a penalty function, our choice being the hyperbolic penalty function.

$${\rm argmin(U)} = {\rm hyp}(\mathbf{r}) = \sum_t H(r_t) \vspace{-.1cm}$$ (6)

where $H(r) = \sqrt{ r^2 + R^2}-R$ , and $R$ is the $\ell_1/\ell_2$ threshold parameter.

Take the gradient of the penalty function assuming there is only one variable, $u_3$ giving a single regression equation:

$$\approx \sum_t \frac{\partial H}{\partial r} \frac{\partial r}{\partial u_3} = \frac{\partial r}{\partial u_3} \frac{\partial H}{\partial r}$$ 0 (7)

$$\approx \sum_t ({\rm FT}^{-1} \ D(\omega)\ \frac{\partial}{\partial u_3}\ e^{U(Z)} )_t \ H'(r_t)$$ 0 (8)

$$\approx \sum_t ({\rm FT}^{-1}\ D(\omega)\ Z^3\ e^{U(Z)})_t \ H'(r_t)$$ 0 (9)

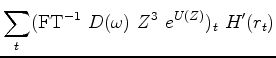so the deconvolution output selected at time $t+3$ multiplies $H'(r_t)$ (also known as the ``soft-clip'' function).

Equation (9) requires us to do an inverse Fourier transform to find the gradient for only $u_3$ . For $u_4$ there is an analogous expression, but it is time shifted by $Z^4$ instead of $Z^3$ . Clearly we need only do one Fourier transform and then shift it to get the time function required for other filter lags. Thus the gradient for all nonzero lags is:

$$0 \approx \Delta\mathbf{u} = (\Delta u_\tau) = (\sum_t \ r_{t+\tau} \ H'(r_t))$$ (10)

$$\Delta U = \ \overline{{\rm FT}(\mathbf{r})} {{\rm\ FT}({\rm softclip}(\mathbf{r}))}$$ (11)

where $\tau$ measures some filter lag. Actually, equation (11) is wrong as it stands. Conceptually it should be brought into the time domain and have $\Delta u_0$ set to zero. More simply, the mean can be removed in the Fourier domain.

Equation (10) says if we were doing least squares, the gradient would be simply the autocorrelation of the residual. When the gradient at nonzero lags drops to zero, the residual is white. Hooray! We long understood that limit. What is currently new is that we now have a two-sided filter. Likewise the $\ell_1$ limit must be where the output is uncorrelated with the clipped output at all lags but zero lag.

(I'm finding it fascinating to look back on what we did all these years with the causal filter $A(Z)$ and comparing it to the non-causal exponential filter $e^{U(Z)}$ . In an $\ell_2$ norm world for filter $A(Z)$ we easily saw the shifted output was orthogonal to the fitting function input. For filter $e^{U(Z)}$ we easily see now the shifted output is orthogonal to the output. The whiteness of the output comes easily with $e^{U(Z)}$ but with $A(Z)$ the Claerbout (2011) contains a lengthy and tricky proof of whiteness.)

Let us figure out how a scaled gradient $\alpha\Delta \mathbf{u}$ leads to a residual modification $\alpha\Delta \mathbf{r}$ . The expression $e^U$ is in the Fourier domain. We first view a simple two term example.

$$e^{\alpha\Delta U} = e^{\alpha(\Delta u_1 Z + \Delta u_2 Z^2)}$$ (12)

$$e^{\alpha\Delta U} = 1 + \alpha (\Delta u_1 Z +\Delta u_2 Z^2) + \alpha^2(\cdots)$$ (13)

$${\rm FT}^{-1}\ e^{\alpha\Delta U} = (1 , \alpha \Delta u_1 , \alpha\Delta u_2 ) + \alpha^2(\cdots)$$ (14)

With that background, ignoring $\alpha^2$ , and knowing the gradient $\Delta \mathbf{u}$ , let us work out the forward operator to find $\Delta \mathbf{r}$ . Let ``$\ast$ '' denote convolution.

$$\mathbf{r} + \alpha \Delta \mathbf{r} = {\rm FT}^{-1}( D e^{ U +\alpha \Delta U})$$ (15)

$$= {\rm FT}^{-1} (De^ U e^{\alpha \Delta U})$$ (16)

$$= {\rm FT}^{-1} (De^ U ) \ast {\rm FT}^{-1} ( e^{\alpha \Delta U})$$ (17)

$$= \mathbf{r} \ast ( 1 , \alpha \Delta \mathbf{u})$$ (18)

$$= \mathbf{r} + \alpha \mathbf{r} \ast \Delta \mathbf{u}$$ (19)

In familiar $\ell_2$ problems we would find $\alpha$ as $\alpha=-(\mathbf{r}\cdot d\mathbf{r})/(d\mathbf{r}\cdot d\mathbf{r})$ , now we must find it by

$${\rm argmin}(\alpha) = H(\mathbf{r} +\alpha \mathbf{r} \ast \Delta \mathbf{u})$$ (20)

This we do by the Newton method which iteratively fits the hyperbola to a parabola.

iterate {
  alpha = - (Sum_i H'(r_i) dr_i ) / ( Sum H''(r_i) dr_i^2 )
  r = r + alpha dr
  }

In the pseudocode above, in the $\ell_2$ limit $H'(r)=r$ and $H''(r)=1$ , so so the first iteration gets the correct $\alpha$ , and changes the residual accordingly so all subsequent $\alpha$ values are zero.

We are not finished because we need to assure the constraint $u_0=0$ . In a linear problem it would be sufficient to set $\Delta u_0=0$ , but here we soon do a linearization which breaks the constraint. In the frequency domain the constraint is $\sum_\omega U = 0$ . We meet this constraint by inserting a constant $\beta$ in equation (15) and chosing $\beta$ to get a zero sum over frequency of $U +\alpha\Delta U + \beta$ . Let $\sum$ denote a normalized summation over frequency. By normalized, I mean $\sum \beta = \beta$ . We must choose $\beta$ so that $0= \sum U +\alpha\sum \Delta U + \beta$ . Clearly, $\beta = -\sum U - \alpha\sum\Delta U$ . Pick up again from equation (15) including $\beta$ .

$${\rm argmin}(\alpha) = H(\ {\rm FT}^{-1} (D e^ U \ e^{\alpha \Delta U} \ e^\beta ) \ )$$ (21)

$$= H(\ {\rm FT}^{-1} (D e^ U \ e^{\alpha \Delta U} \ e^{-\sum U} \ e^{-\alpha\sum \Delta U}) \ )$$ (22)

$$= H(\ {\rm FT}^{-1} (D e^ {U -\sum U} \ \ e^{\alpha (\Delta U -\sum \Delta U)}) \ )$$ (23)

$$= H(\ {\rm FT}^{-1} (D e^ {U -\sum U}) \ \ast \ {\rm FT}^{-1} (e^{\alpha (\Delta U -\sum \Delta U)}) \ )$$ (24)

Proceed now along the lines of equation (17) through (20), but with means removed in Fourier space leading to slightly different vectors $\tilde{\mathbf{r}}$ and $\Delta\tilde{\mathbf{u}}$

$${\rm argmin}(\alpha) = H(\ \tilde{\mathbf{r}} + \alpha \tilde{\mathbf{r}} \ast \Delta \tilde{\mathbf{u}} \ )$$ (25)

which is solveable by the method of the same pseudocode above.

A log spectral approach to bidirectional deconvolution