 |
 |
 |
 | Wave-equation inversion of time-lapse seismic data sets |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: APPENDIX A
Previous: Joint Inversion of Multiple
Because in the JMI formulation, the models are completely decoupled, they can be regularized by minimizing the norm
![\begin{displaymath}\begin{array}{ccc} \left \vert\left\vert \left [ \begin{array...
...rray} \right ] \right \vert \right \vert \approx 0 \end{array},\end{displaymath}](img117.png) |
(A-32) |
where
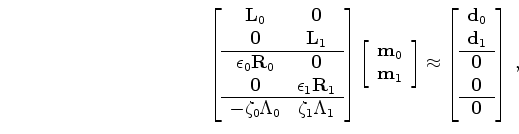 is the spatial regularization operator and
is the spatial regularization operator and
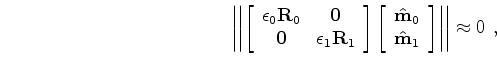 the spatial regularization parameter for survey
the spatial regularization parameter for survey 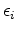 .
To add any temporal regularization, we need to warp the inverted monitor images to the baseline and then apply temporal constraints
or we can regularize the time-lapse image directly by minimizing the norm:
.
To add any temporal regularization, we need to warp the inverted monitor images to the baseline and then apply temporal constraints
or we can regularize the time-lapse image directly by minimizing the norm:
![\begin{displaymath}\begin{array}{ccc} \left \vert\left\vert \left [ \begin{array...
...rray} \right ] \right \vert \right \vert \approx 0 \end{array},\end{displaymath}](img120.png) |
(A-33) |
where
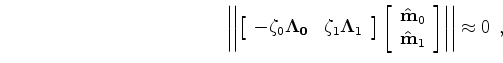 is the temporal regularization operator and
is the temporal regularization operator and 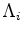 is the regularization parameter.
Therefore the full regularized inversion requires a minimization of the norm:
is the regularization parameter.
Therefore the full regularized inversion requires a minimization of the norm:
![\begin{displaymath}\begin{array}{ccc} \left \vert\left\vert \left [ \begin{array...
...rray} \right ] \right \vert \right \vert \approx 0 \end{array},\end{displaymath}](img123.png) |
(A-34) |
which leads to the image-space problem
![\begin{displaymath}\begin{array}{c} \left [ \begin{array}{ccc} {\bf H }_{0} & {\...
...\\ \hline {\bf0} \\ {\bf0} \\ \end{array} \right ], \end{array}\end{displaymath}](img124.png) |
(A-35) |
where
 and
and
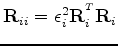 are the spatial and temporal constraints, respectively.
are the spatial and temporal constraints, respectively.
If the monitor has been aligned to the baseline, then we can impose the spatial regularization by minimizing
![\begin{displaymath}\begin{array}{ccc} \left \vert\left\vert \left [ \begin{array...
...rray} \right ] \right \vert \right \vert \approx 0 \end{array},\end{displaymath}](img117.png) |
(A-36) |
and the temporal regularization by minimizing
![\begin{displaymath}\begin{array}{ccc} \left \vert\left\vert \left [ \begin{array...
...rray} \right ] \right \vert \right \vert \approx 0 \end{array},\end{displaymath}](img120.png) |
(A-37) |
where
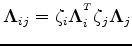 and
and
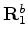 are defined with respect to the baseline-aligned monitor image.
If the time-lapse image at the baseline position, the regularized image-space inversion problem is given by
are defined with respect to the baseline-aligned monitor image.
If the time-lapse image at the baseline position, the regularized image-space inversion problem is given by
![\begin{displaymath}\begin{array}{c} \left [ \begin{array}{ccc} {\bf H }_{0} & {\...
...\\ \hline {\bf0} \\ {\bf0} \\ \end{array} \right ], \end{array}\end{displaymath}](img26.png) |
(A-38) |
where the superscript 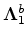 denotes that the operators and images are referenced to the baseline position.
Note that in the simplest case, where the temporal regularization is a difference operator equation A-33 becomes
denotes that the operators and images are referenced to the baseline position.
Note that in the simplest case, where the temporal regularization is a difference operator equation A-33 becomes
![\begin{displaymath}\begin{array}{ccc} \left \vert\left\vert \zeta \left [ \begin...
...rray} \right ] \right \vert \right \vert \approx 0 \end{array},\end{displaymath}](img130.png) |
(A-39) |
and for the baseline-aligned images, the temporal constraint in equation A-37 becomes
![\begin{displaymath}\begin{array}{ccc} \left \vert\left\vert \zeta \left [ \begin...
...rray} \right ] \right \vert \right \vert \approx 0 \end{array}.\end{displaymath}](img131.png) |
(A-40) |
 |
 |
 |
 | Wave-equation inversion of time-lapse seismic data sets |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: APPENDIX A
Previous: Joint Inversion of Multiple
2011-05-24
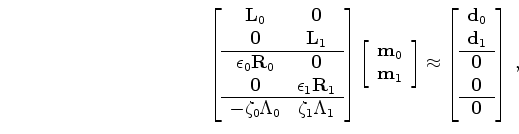 is the spatial regularization operator and
is the spatial regularization operator and
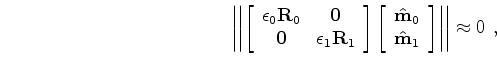 the spatial regularization parameter for survey
the spatial regularization parameter for survey 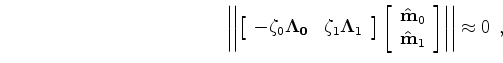 is the temporal regularization operator and
is the temporal regularization operator and  and
and