A new bidirectional deconvolution method that overcomes the minimum phase assumption

Inverting a single wavelet

To verify the bidirectional deconvolution's ability to handle mixed-phase wavelets, we first set the input data to be a single wavelet, to see whether the data can be compressed to a single spike. We choose three types of wavelets as inputs:

1. a minimum-phase wavelet used in the previous report (Zhang and Claerbout, 2010), referred to as wavelet 1.
2. a wavelet that deviates slightly from minimum-phase: it models a simple marine ghost - a low frequency function passing through a time derivative at the source and another at the receiver. The low frequency function chosen is the convolution of two one-sided triangles.
3. a zero-phase wavelet created by convolving the minimum-phase with its own time-reverse wavelet. Such wavelet has identical $a$ and $b$ components, referred to as wavelet 3.

minwavlet,mod-minwavlet,jonwavlet,mod-jonwavlet,symwavlet,mod-symwavlet
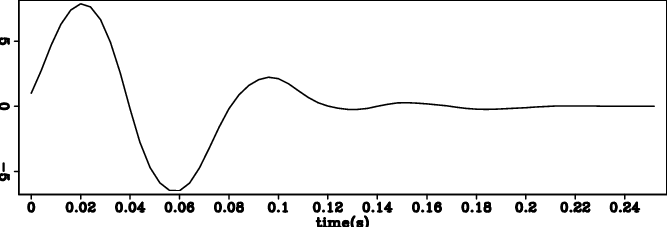
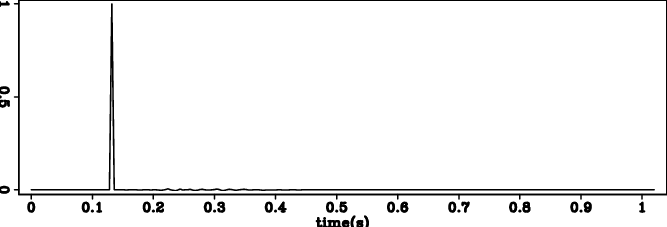
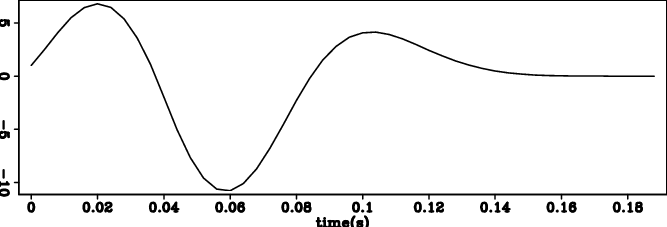
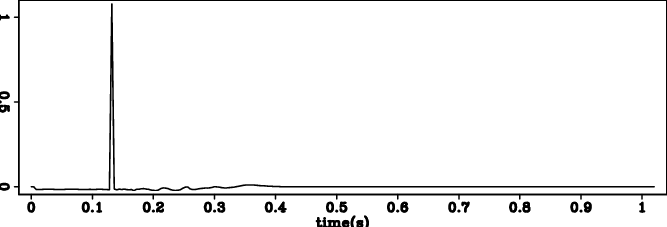
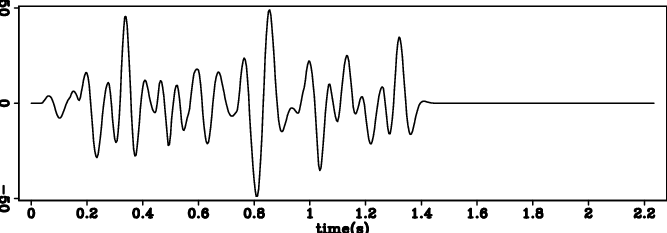
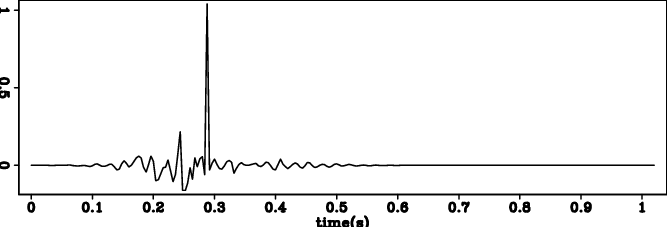
Figure 1. (a) Input wavelet 1 and (b) its deconvolution result. (c) Input wavelet 2 and (b) its deconvolution result. (e) Input wavelet 3 and (f) its deconvolution result.

fita-symwavlet,fitb-symwavlet
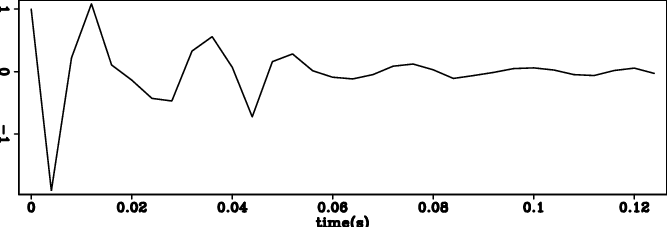
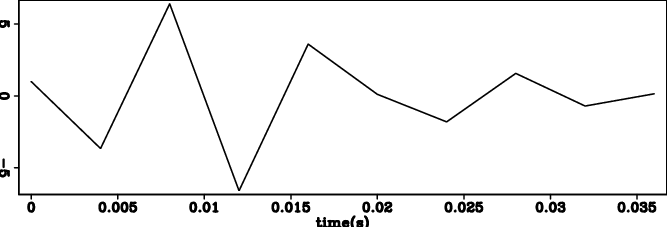
Figure 2. For the wavelet 3 inversion, (a) filter $f_a$ ; (b) filter $f_b$ .

Figure 1(a) 1(b), figure 1(c) 1(d) and figure 1(e) 1(f) show wavelets 1,2,3, and the results of reflectivity models respectively. In all 3 cases, our bidirectional deconvolution method is able to compress the wavelet into a spike.

Figure 2 shows the retrieved filters $f_a$ and $f_b$ from wavelet 3's inversion. Notice that $f_a$ and $f_b$ given by the inversion are different from each other, while ideally they should be the same, since $a$ and $b$ are the same when we create wavelet 3. This observation indicates that the solutions $f_a$ and $f_b$ of this method do not necessarily converge to the inverse of the initial $a$ and $b$ .

A new bidirectional deconvolution method that overcomes the minimum phase assumption