 |
 |
 |
 | Hybrid-norm and Fortran 2003: Separating the physics from the solver |  |
![[pdf]](icons/pdf.png) |
Next: Implementation in Fortran 2003
Up: Hybrid-norm and Fortran 2003:
Previous: Solvers
The L2-norm is often a non-optimal choice both because of the non-Gaussian
nature of noise in data and
it's tendency to create smooth models with traditional regularization
schemes. To improve model estimation, authors have suggested using either
direct L1-norm approaches, or more commonly, Iteratively Reweighed Least-Squares
(IRLS) to approximate different norms. IRLS attempts
to find the best model at a non-L2 norm by a series of linearization s.
Each non-linear iteration updates the weighting 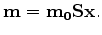 of the residual. For example we can achieve L1 like behavior by updating
the weighting operator through,
of the residual. For example we can achieve L1 like behavior by updating
the weighting operator through,
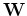 |
(10) |
IRLS methods tend to be difficult to use because the user must
choose carefully the number of relinearizations and the numbers of steps
between relinearizations carefully.
(Claerbout, 2009) suggested an alternate approach that
dynamically changes the weighting function every iteration and uses a Taylor expansion
of the standard conjugate direction algorithm to update the solution. Further he
suggests a different norm, the hybrid norm, that creates a smooth transition between the
standard L2 problem and a L1 problem.
Given an error function 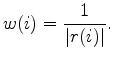 and a residual vector
and a residual vector
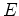 the hybrid norm is defined
the hybrid norm is defined
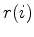 |
(11) |
where 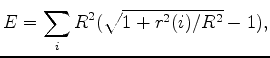 is a user supplied bad-data percentile.
is a user supplied bad-data percentile.
Creating an inversion framework that supports a Taylor expansion approach
to conjugate directions requires adding two additional features to our
vector class description. First, we need to associate a norm to each vector.
Second we need to be able to multiply a vector by another vector, element
by element.
Adding support for the hybrid norm requires more changes. A vector
must now have a bad-data percentage associated with it, it must be
able to find its ith percentile value, and create a vector
with this value.
 |
 |
 |
 | Hybrid-norm and Fortran 2003: Separating the physics from the solver |  |
![[pdf]](icons/pdf.png) |
Next: Implementation in Fortran 2003
Up: Hybrid-norm and Fortran 2003:
Previous: Solvers
2010-11-26
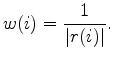 and a residual vector
and a residual vector
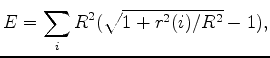 is a user supplied bad-data percentile.
is a user supplied bad-data percentile.