 |
 |
 |
 | Hybrid-norm and Fortran 2003: Separating the physics from the solver |  |
![[pdf]](icons/pdf.png) |
Next: Operators
Up: Operator-based object-oriented solvers
Previous: Operator-based object-oriented solvers
The solver writer
doesn't need to know anything about 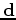 other than how
to apply it and it's adjoint. In fact, the solver writer doesn't
need to know much about
other than how
to apply it and it's adjoint. In fact, the solver writer doesn't
need to know much about  or
or 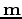 .
The steepest descent approach described above involves only three
mathematical operations. In order to find the best scaling factor
.
The steepest descent approach described above involves only three
mathematical operations. In order to find the best scaling factor
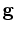 , we need to calculate a dot product. In order to update the
model and the residual, we will need to scale
, we need to calculate a dot product. In order to update the
model and the residual, we will need to scale 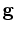 and
add it to
and
add it to 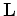 .
We can define the interface
for calling the forward of
.
We can define the interface
for calling the forward of 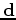 as
as
call lop (logical add, vec m, vec d)
If the class vec has the ability to perform the add,
scale, and dot product functions, we can begin to write
a generic solver. Two more initialization functions are needed in
the class vec. We need to be able to create the gradient
vector before we can apply the adjoint. As a result, we need
to be able to create a vector with the same number of elements as
the model. Put another way, we need to clone the model.
We also need to be able to zero this vector, or set the vector
to some value.
There are several other functions that can be useful
in a generic vector class. The ability
to check that two vectors are from
the same vector space can avoid many
bugs. The ability to fill the vector
with random numbers makes it easy to test whether or not
an operator passes the dot product. Scaling and adding
are often done together by defining a scale-add feature,
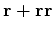 |
(2) |
that updates a vector 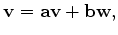 by scaling it with a
scaled version of a second vector
by scaling it with a
scaled version of a second vector  we can often
improve performance.
Finally, having the ability to make a copy of only
the space a vector sits in rather than making copy of
all elements can often improve performance and reduce
storage requirements.
we can often
improve performance.
Finally, having the ability to make a copy of only
the space a vector sits in rather than making copy of
all elements can often improve performance and reduce
storage requirements.
 |
 |
 |
 | Hybrid-norm and Fortran 2003: Separating the physics from the solver |  |
![[pdf]](icons/pdf.png) |
Next: Operators
Up: Operator-based object-oriented solvers
Previous: Operator-based object-oriented solvers
2010-11-26