 |
 |
 |
 | Wave-equation migration velocity analysis by residual moveout fitting |  |
![[pdf]](icons/pdf.png) |
Next: Conclusions
Up: Theory
Previous: Derivatives of moveout parameters
The computational cost and storage overheads for evaluating
terms II and III in the gradient expression 16
are limited because only operations on the prestack
image are required.
On the contrary,
the computation of term I is computationally more demanding.
It requires the forward propagation and backward propagation of wavefields.
The application of
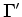 and
and
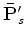 requires the storage, and retrieval,
of the source wavefield and receiver wavefield.
Furthermore,
to apply
requires the storage, and retrieval,
of the source wavefield and receiver wavefield.
Furthermore,
to apply
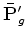 and
and
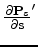 we need to correlate the source and receiver wavefields
with the wavefields generated by the image derivatives.
In summary, the computational cost of one gradient computation
of the proposed method
can be roughly estimated to be twice the computational cost
of one gradient computation of a full-waveform inversion algorithm.
The factor of two occurs because two propagations
are needed to backproject the image perturbations
into the slowness model along both
the source wavepaths and the receiver wavepaths.
we need to correlate the source and receiver wavefields
with the wavefields generated by the image derivatives.
In summary, the computational cost of one gradient computation
of the proposed method
can be roughly estimated to be twice the computational cost
of one gradient computation of a full-waveform inversion algorithm.
The factor of two occurs because two propagations
are needed to backproject the image perturbations
into the slowness model along both
the source wavepaths and the receiver wavepaths.
The data-handling task could be simplified if the
frequency-domain downward-continuation migration is used instead
of reverse-time migration,
because computations can be performed independently
for each frequency.
The adaptation of the theory presented in this paper
to downward-continuation migration is fairly straightforward.
It would only require to exchange expressions 1
and A-4 with the corresponding frequency-domain
expressions.
 |
 |
 |
 | Wave-equation migration velocity analysis by residual moveout fitting |  |
![[pdf]](icons/pdf.png) |
Next: Conclusions
Up: Theory
Previous: Derivatives of moveout parameters
2010-11-26