|
|
|
|
Wave-equation migration velocity analysis by residual moveout fitting |
The derivatives of 4 with respect to the vector of moveout parameters is easily evaluated using the following expression:
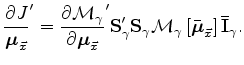 can be represented as a
can be represented as a
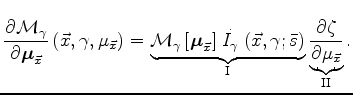 after moveout.
This term can be numerically evaluated by
applying to the moved-out image
a finite-difference approximation of the first-derivative operator.
The second term (II) is different from zero
only when the spatial coordinate
after moveout.
This term can be numerically evaluated by
applying to the moved-out image
a finite-difference approximation of the first-derivative operator.
The second term (II) is different from zero
only when the spatial coordinate
The preceding expression simplifies
when the gradient is evaluated for
![]() .
This simplifying condition is actually always fulfilled
unless the optimization algorithm includes inner iterations
for fitting the moveout parameters using a linearized approach.
Under this condition,
equation 8 becomes
.
This simplifying condition is actually always fulfilled
unless the optimization algorithm includes inner iterations
for fitting the moveout parameters using a linearized approach.
Under this condition,
equation 8 becomes
|
|
|
|
Wave-equation migration velocity analysis by residual moveout fitting |