Gradient of the objective function

Next: Derivatives of objective function Up: Theory Previous: Theory

Gradient of the objective function

I plan to solve the optimization problem defined in 4 by a gradient-based optimization algorithm. Therefore, the development of an algorithm for efficiently computing the gradient of the objective function with respect to slowness is an essential step to make the method practical. In this section I outline the methodology to compute the gradient, and I leave some of the details to Appendix A.

The gradient is computed using the chain rule. The first term of the chain is the derivative of the objective function in equation 4 with respect the moveout parameters. The second term is the derivatives of the moveout parameters with respect to slowness that are computed from the objective function 5.

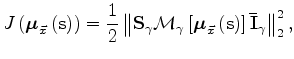Subsections

Derivatives of objective function ( ) with respect to moveout parameters ( ${\boldsymbol \mu}_{\vec x}$ )
Derivatives of moveout parameters ( ${\boldsymbol \mu}_{\vec x}$ ) with respect to slowness ( ${\bf {s}}$ )

2010-11-26