|
|
|
|
Dix inversion constrained by L1-norm optimization |
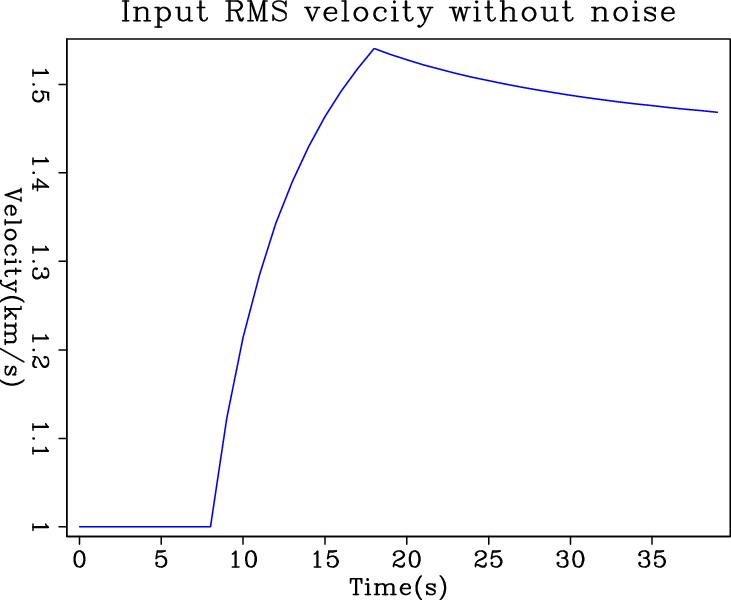
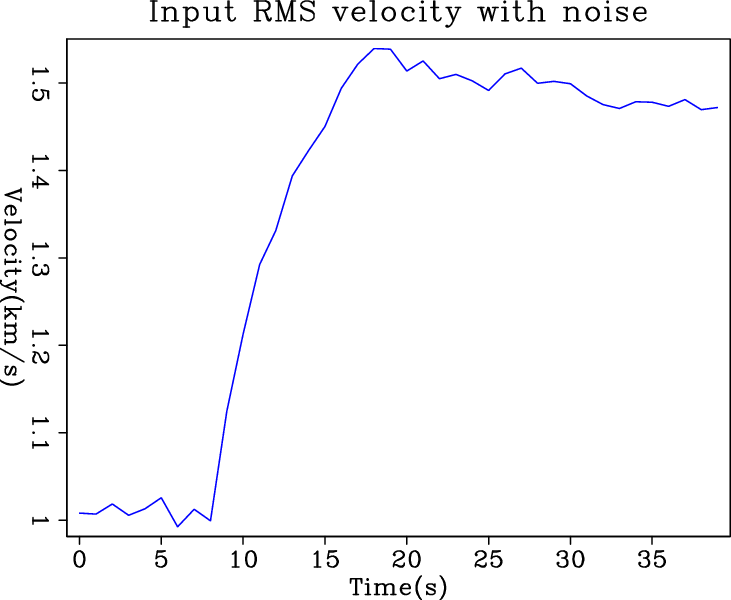
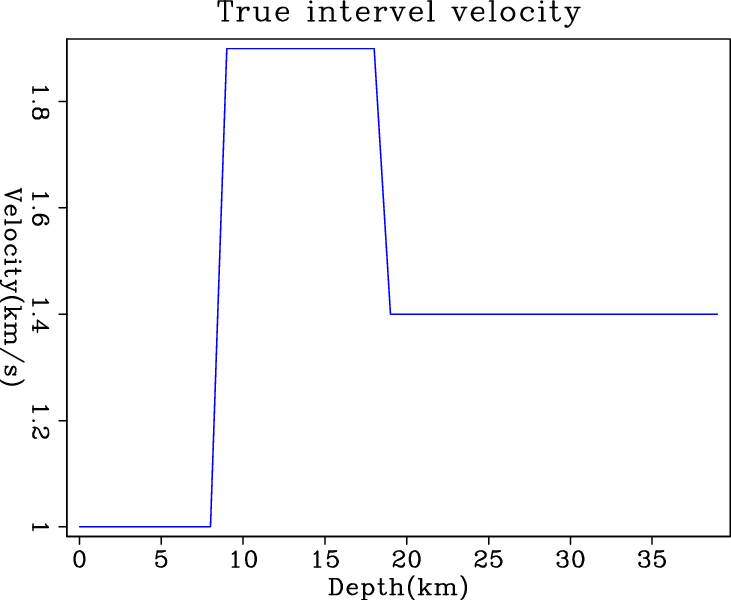
Figure 1 shows the input synthetic RMS velocities with and without random noise, and the true blocky interval velocity we try to invert for. For the synthetic problem, we experimented on solvers with and without regularization to learn the nature of the solver itself and the nature of its regularization.
Figure 2 shows the inversion results when
clean data (free of noise) are fed into different simple solvers
without any regularization. The result of ![]() regression is comparable to the
IRLS and hybrid norm. However,
the simple conjugate direction
regression is comparable to the
IRLS and hybrid norm. However,
the simple conjugate direction ![]() solver failed to give a satisfactory result
(Figure 2(c)). As we have discussed in the previous
section, this might be due to the flat bottom caused by the data
configuration.
solver failed to give a satisfactory result
(Figure 2(c)). As we have discussed in the previous
section, this might be due to the flat bottom caused by the data
configuration.
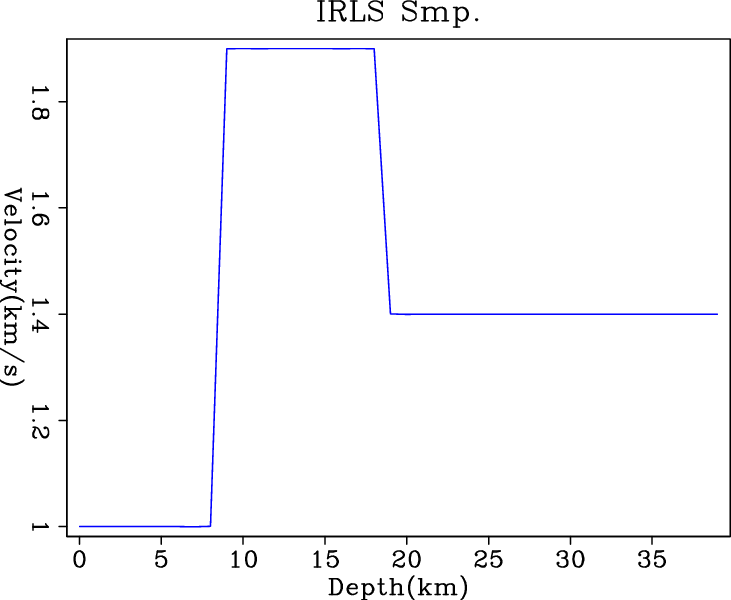
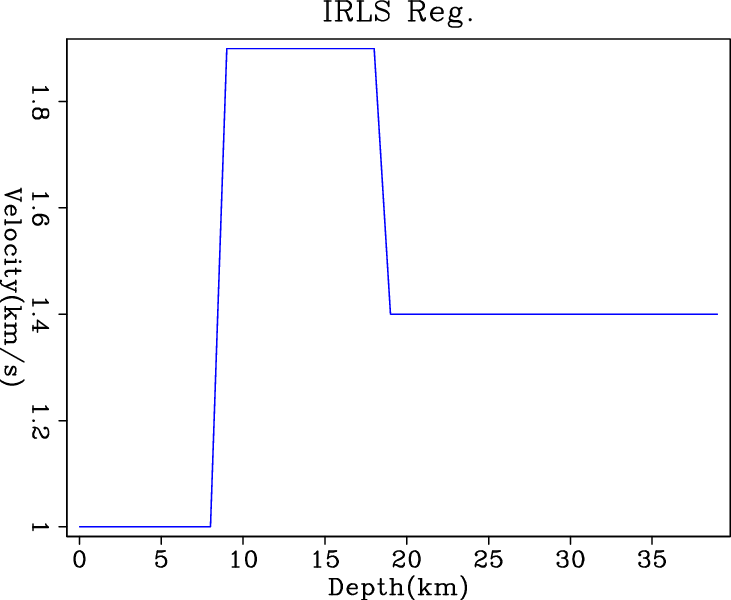
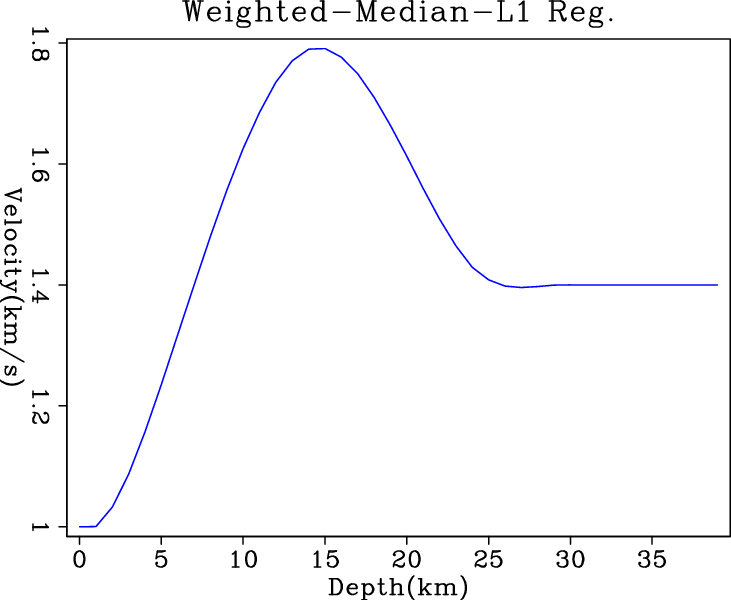
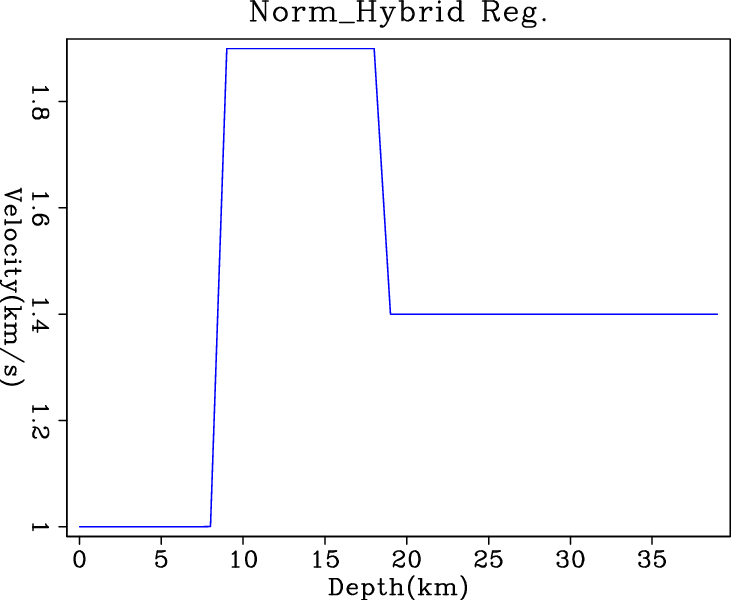
Figure 3 shows the inversion results when
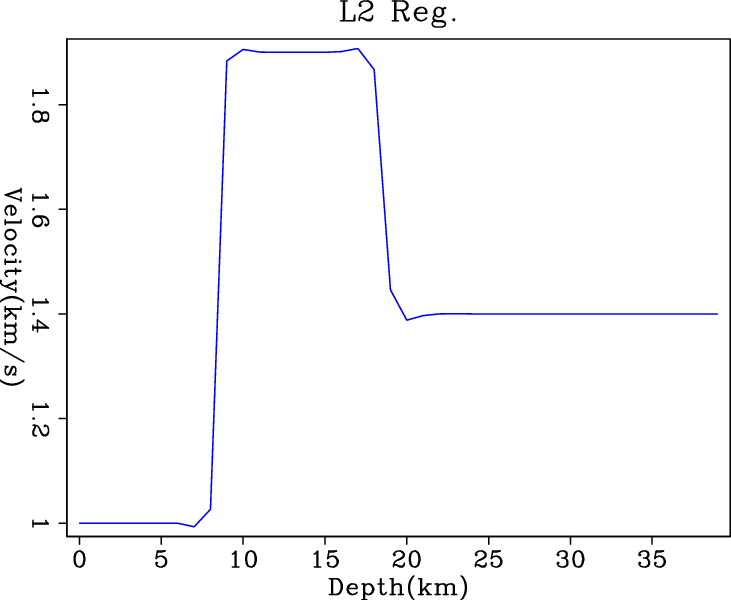
clean data are fed into different regularized solvers. As expected, the
smoothing effect of ![]() regularization on the derivative of model
produces the round corners at the turning point. In contrast,
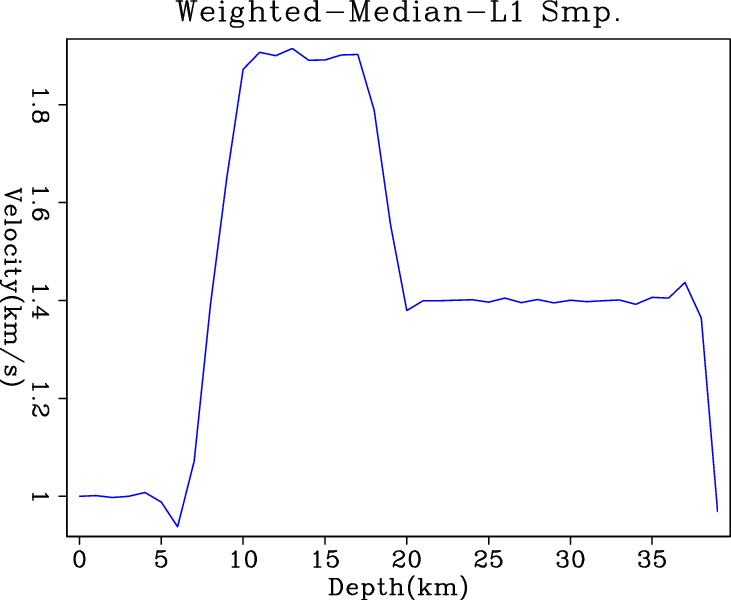
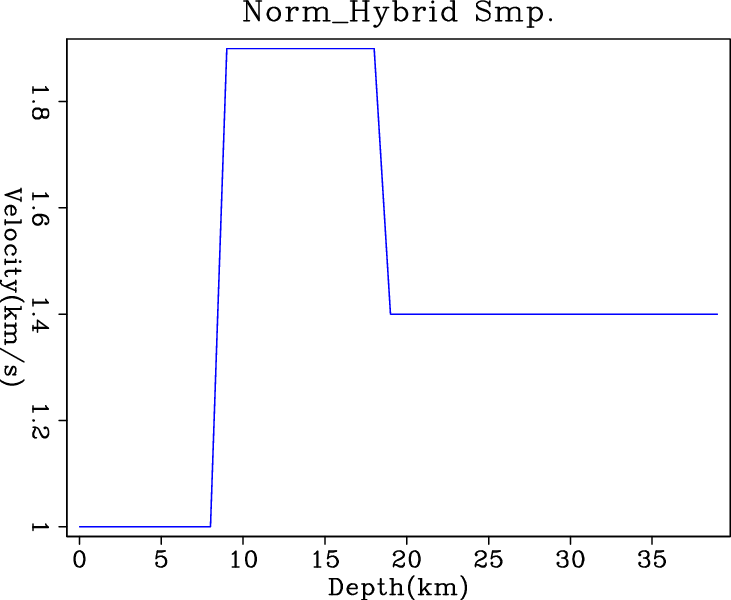
IRLS and hybrid solvers give perfect exact solutions, which benefit
from their
regularization on the derivative of model
produces the round corners at the turning point. In contrast,
IRLS and hybrid solvers give perfect exact solutions, which benefit
from their ![]() nature in regularization. We do not fully understand
the behavior of conjugate-direction
nature in regularization. We do not fully understand
the behavior of conjugate-direction ![]() solver, but the change in
the result can be explained by the change of the data configuration
when the regularization term is added.
solver, but the change in
the result can be explained by the change of the data configuration
when the regularization term is added.
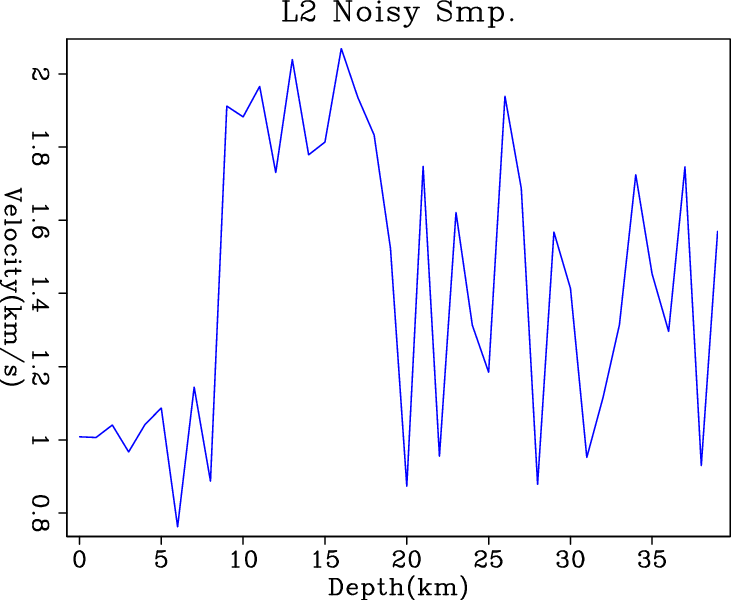
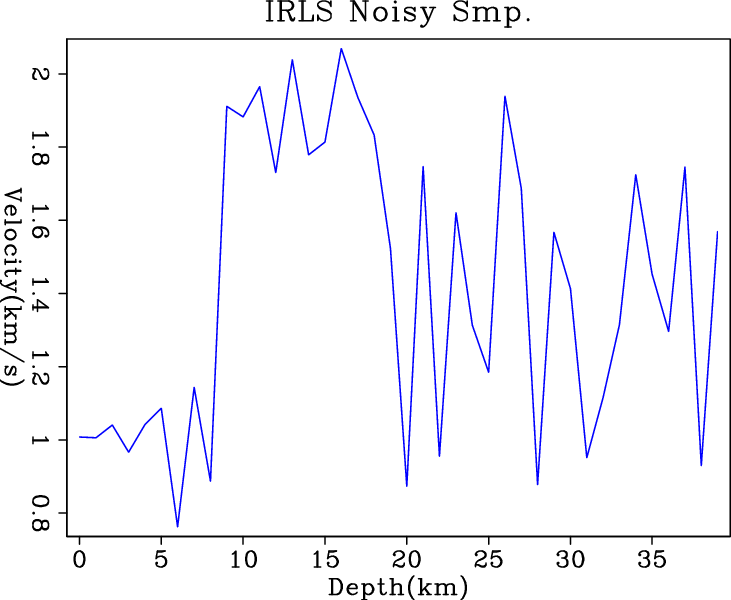
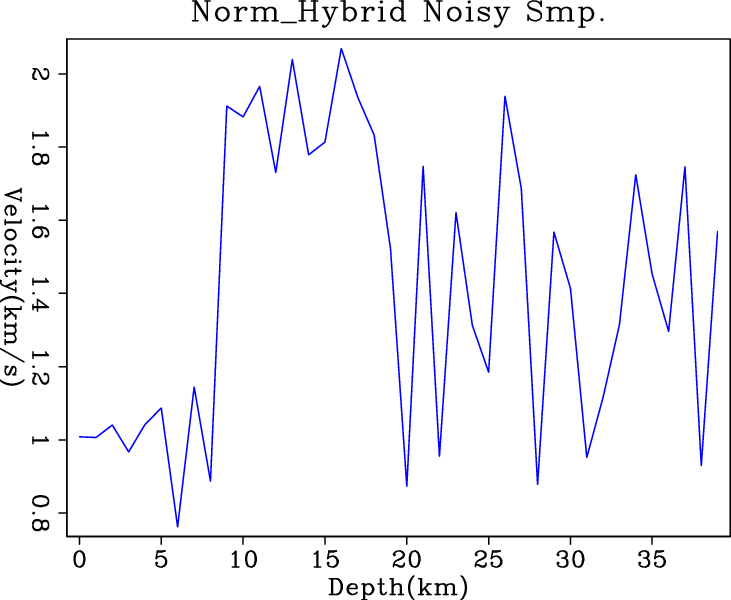
Figure 4 shows the inversion results when
noisy data are fed into different simple solvers without any
regularization. When creating the synthetic noisy RMS velocity data,
uniform distributed random noise is added. However, ![]() norm assumes
Gaussian noise, and
norm assumes
Gaussian noise, and ![]() minimization is
derived under the assumption of exponential distribution. Therefore, the
simple
minimization is
derived under the assumption of exponential distribution. Therefore, the
simple ![]() solver, the IRLS solver or hybrid solver all fail to
recognize the noise and attenuate it. Surprisingly,
conjugate-direction
solver, the IRLS solver or hybrid solver all fail to
recognize the noise and attenuate it. Surprisingly,
conjugate-direction ![]() solver successfully eliminates the
high-frequency noise and keeps the low-frequency trend of the interval
velocity function. It shows great potential for finding the exact
solution when the problem is slightly more complicated.
solver successfully eliminates the
high-frequency noise and keeps the low-frequency trend of the interval
velocity function. It shows great potential for finding the exact
solution when the problem is slightly more complicated.
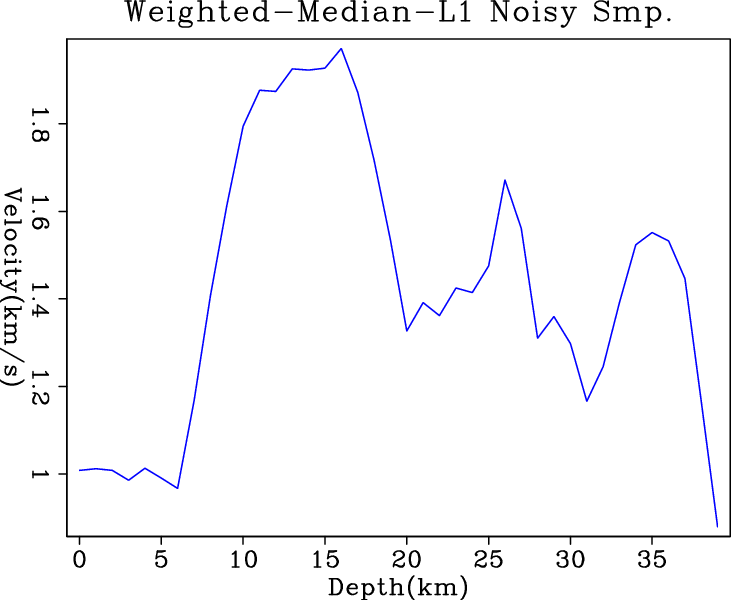
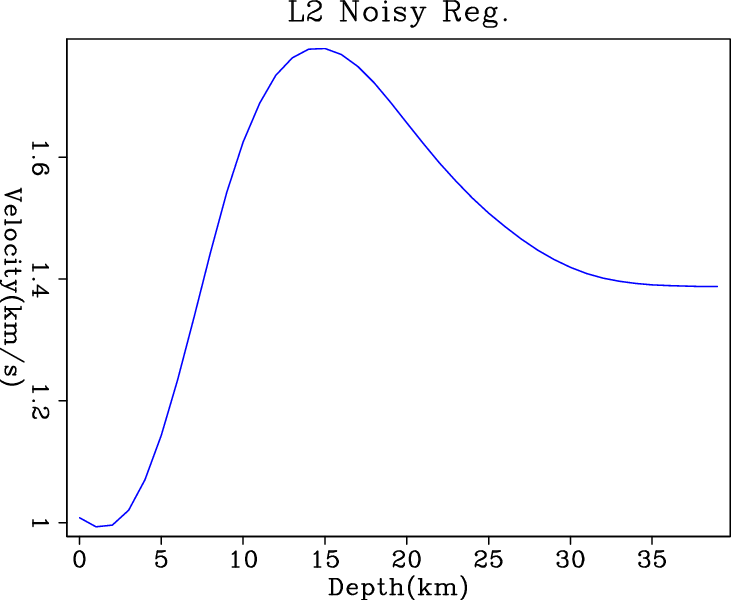
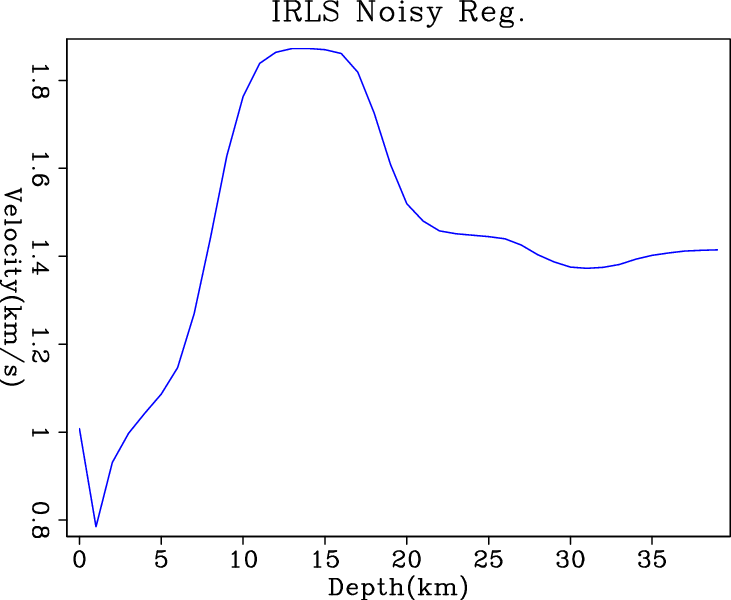
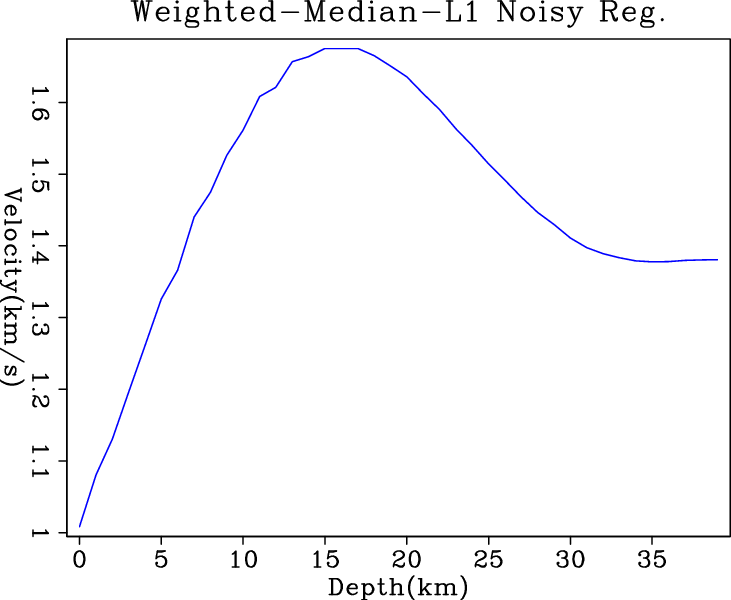
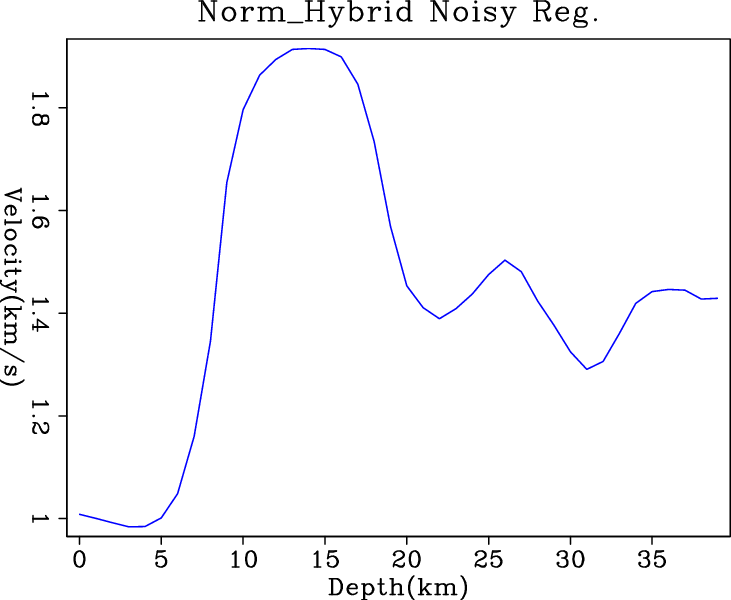
Figure 5 shows the inversion results when
noisy data are fed into different regularized solvers. By adding this
regularization term to further constrain the problem, we expect better
results out of each solver. Comparing the results in Figure
5, IRLS result has the most
blocky transition between layers and is almost flat within the layers. However, the big jump at shallower depths is apparently due to
its tolerance of the large residuals. The hybrid solver gives result
comparable to the IRLS, but it oscillates at deeper depths. The results from ![]() and conjugate direction
and conjugate direction
![]() solver are similar, but the smaller steps in the result of
conjugate direction
solver are similar, but the smaller steps in the result of
conjugate direction ![]() (Figure 5(c)) are promising.
(Figure 5(c)) are promising.
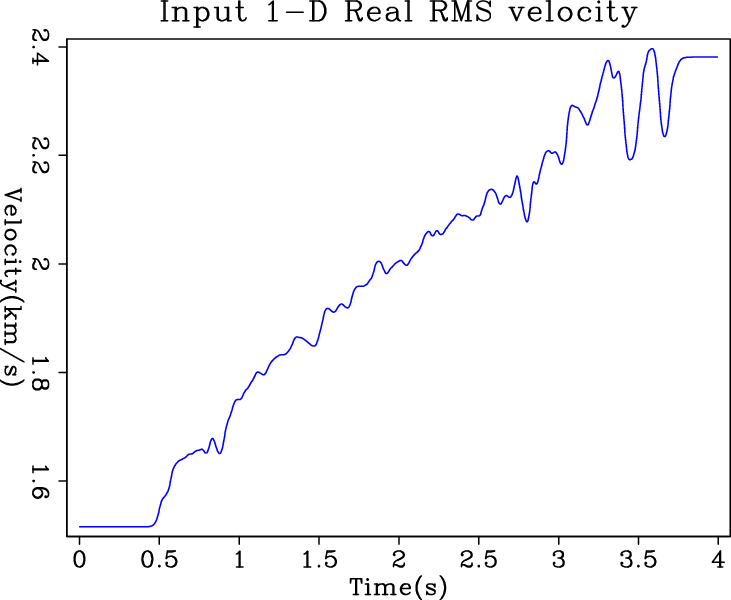
Figure 6 shows the 1-D field RMS velocity from the velocity scan. This field data has 1,000 sample points, and the number of blocks in the model space is unknown. In real life, we can never fully constrain a inversion problem without regularization: that is when Dix inversion becomes unstable. Therefore, only regularized solvers are tested.
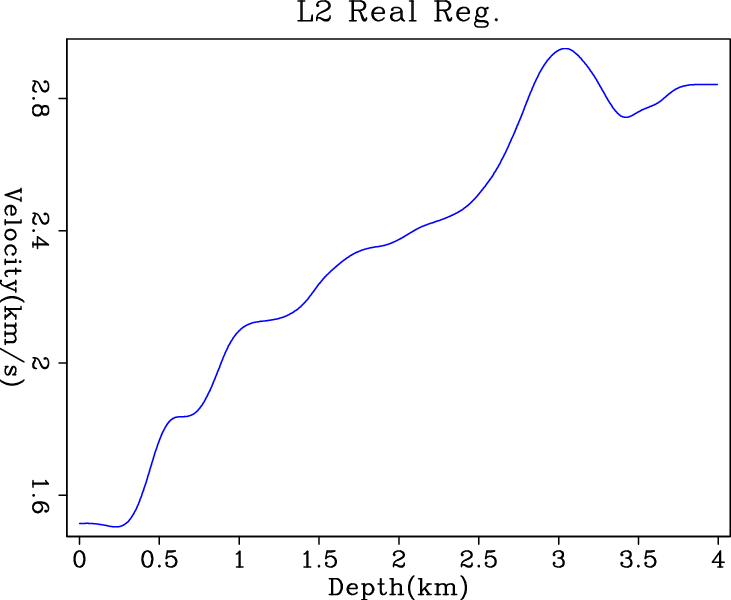
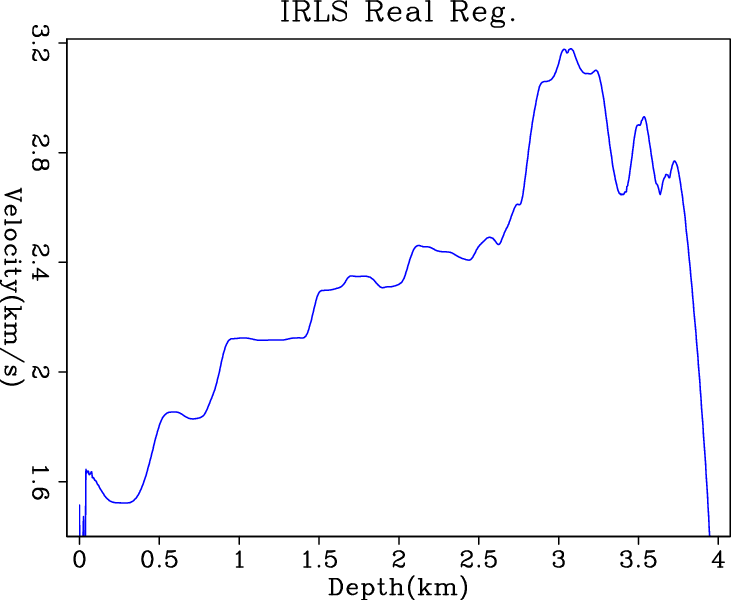
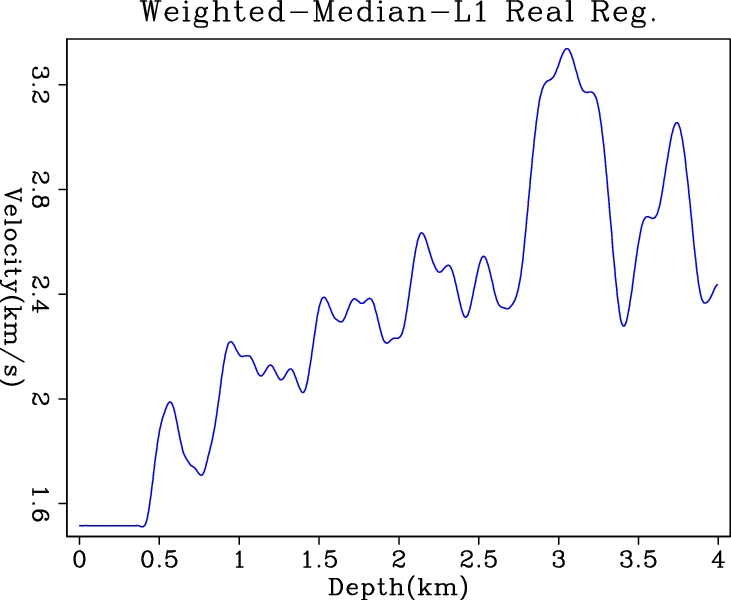
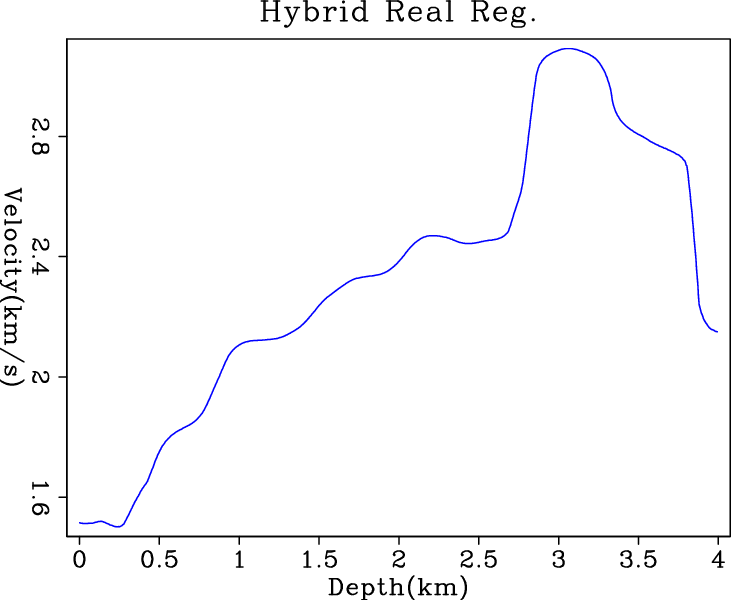
Figure 7 shows the inversion results
when field data in Figure 6 are fed into different
regularized solvers. The results from the IRLS and the conjugate
direction ![]() solver have more blocky nature than the other
two. The result from IRLS is more flat within layers, which is a nice
property in well-log matching and many other geophysical
applications. The hybrid and
solver have more blocky nature than the other
two. The result from IRLS is more flat within layers, which is a nice
property in well-log matching and many other geophysical
applications. The hybrid and ![]() solvers give comparable
results, although we have chosen a very small
solvers give comparable
results, although we have chosen a very small ![]() for hybrid
norm to force it towards the
for hybrid
norm to force it towards the ![]() norm.
norm.
|
|---|
|
rmsvel,rms-noise,intervel
Figure 1. Input synthetic RMS velocity and true interval velocity. The two plots on the top row are the input RMS velocities (a) without noise and (b) with random noise, respectively. The plot on the bottom is (c) the true interval velocity which is true model in the estimation problem. [ER] |
|
|
|
|---|
|
l21,irls1,wmed1,nrm3
Figure 2. Inversion results of simple (a) |
|
|
|
|---|
|
l22,irls2,wmed2,nrm2
Figure 3. Inversion results of (a) |
|
|
|
|---|
|
l23,irls3,wmed4,nrm5
Figure 4. Inversion results of simple (a) |
|
|
|
|---|
|
l24,irls4,wmed5,nrm6
Figure 5. Inversion results of (a) |
|
|
|
realrms
Figure 6. Input 1-D field RMS velocity data from velocity scan. [ER] |
|
|---|---|
|
|
|
|---|
|
real2,real1,real4,real6
Figure 7. Inversion results of (a) |
|
|
|
|
|
|
Dix inversion constrained by L1-norm optimization |