 |
 |
 |
 | Kinematics in iterated correlations of a passive acoustic experiment |  |
![[pdf]](icons/pdf.png) |
Next: Example of Green's function
Up: De Ridder and Papanicolaou:
Previous: Green's function retrieval by
The phase of the correlation under the integral on the right-hand side of equation 2 changes rapidly as a function of source position. The dominant contribution to the integral comes from points at which the phase is stationary. Physically these positions correspond to source points from where the ray paths to both stations align. To analyze the stationary phases in the presence of a scatterer, we consider a homogeneous medium and study the time-domain expression of equation 2 using the first three terms in
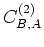 of equation 4:
of equation 4:
where 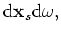 and
and 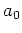 are amplitude factors. The rapid phases,
are amplitude factors. The rapid phases,
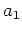 ,
,
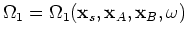 and
and
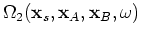 , of the three terms are found using equations A-6 and A-11:
, of the three terms are found using equations A-6 and A-11:
where
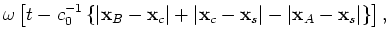 is the position of the scatterer.
is the position of the scatterer.
We analyze these rapid phases using the stationary-phase method, keeping
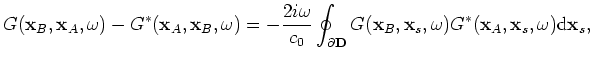 and
and
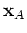 fixed and varying
fixed and varying
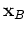 . According to the stationary-phase method, the dominant contribution comes from stationary phases where
. According to the stationary-phase method, the dominant contribution comes from stationary phases where
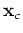 |
(14) |
From the rapid phase, 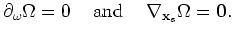 , of the first term in equation 6, we find stationary points for which
, of the first term in equation 6, we find stationary points for which
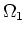 |
|
|
(15) |
The second condition requires the points
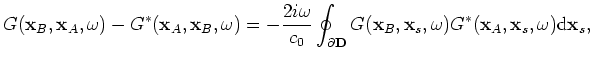 and
and
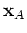 to be aligned along a line issuing from
to be aligned along a line issuing from
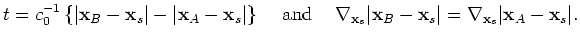 . When the stations and source are aligned as
. When the stations and source are aligned as
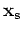 , the first condition gives
, the first condition gives
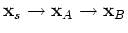 . When the stations and source are aligned as
. When the stations and source are aligned as
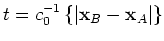 , the first condition gives
, the first condition gives
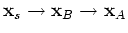 .
.
From rapid phase 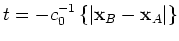 of the second terms in equation 6, we find stationary points for which
of the second terms in equation 6, we find stationary points for which
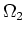 |
|
|
(16) |
The second condition requires the points
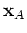 and
and
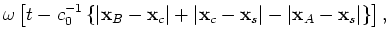 to be on a line issuing from
to be on a line issuing from
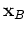 . When station B, as well as the scatterer and sources are aligned as
. When station B, as well as the scatterer and sources are aligned as
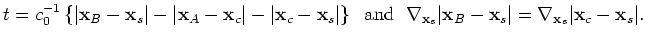 , then
, then
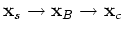 , and the first condition states that
, and the first condition states that
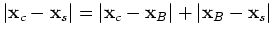 . When station B, the scatterer and the source are aligned as
. When station B, the scatterer and the source are aligned as
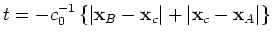 , then
, then
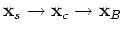 , and the first condition states that
, and the first condition states that
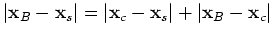 .
.
From rapid phase 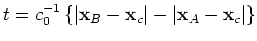 of the second terms in equation 6, we find stationary points for which
of the second terms in equation 6, we find stationary points for which
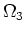 |
|
|
(17) |
The second condition requires the points
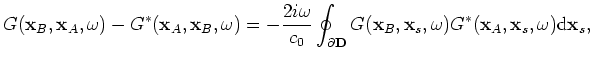 and
and
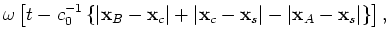 to be on a line issuing from
to be on a line issuing from
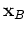 . When station A, as well as the scatterer and sources are aligned as
. When station A, as well as the scatterer and sources are aligned as
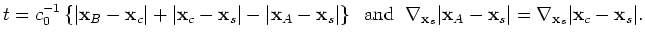 , then
, then
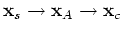 , and the first condition states that
, and the first condition states that
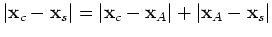 . When station A, the scatterer and sources are aligned as
. When station A, the scatterer and sources are aligned as
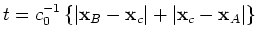 , then
, then
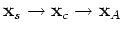 , and the first condition states that
, and the first condition states that
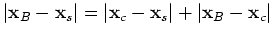 . For a more extensive treatment of stationary-phase positions in conventional interferometry, see Schuster et al. (2004); Snieder et al. (2006); Snieder (2004) and Garnier and Papanicolaou (2009).
. For a more extensive treatment of stationary-phase positions in conventional interferometry, see Schuster et al. (2004); Snieder et al. (2006); Snieder (2004) and Garnier and Papanicolaou (2009).
 |
 |
 |
 | Kinematics in iterated correlations of a passive acoustic experiment |  |
![[pdf]](icons/pdf.png) |
Next: Example of Green's function
Up: De Ridder and Papanicolaou:
Previous: Green's function retrieval by
2009-05-05
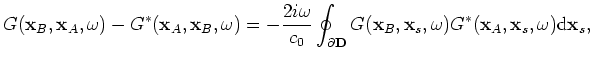 and
and
![]() fixed and varying
fixed and varying
![]() . According to the stationary-phase method, the dominant contribution comes from stationary phases where
. According to the stationary-phase method, the dominant contribution comes from stationary phases where
![]() , of the first term in equation 6, we find stationary points for which
, of the first term in equation 6, we find stationary points for which
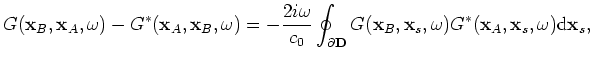 and
and
![]() of the second terms in equation 6, we find stationary points for which
of the second terms in equation 6, we find stationary points for which
![]() of the second terms in equation 6, we find stationary points for which
of the second terms in equation 6, we find stationary points for which
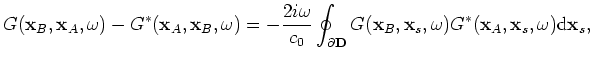 and
and