Source signature and static shifts estimations for multi-component ocean bottom data

Up-down separation using PZ summation

Traditionally, PZ summation is employed to extract the up-going portion of the wavefield with the goal of eliminating water reverberation (Rosales and Guitton, 2004). We use the down-going wavefield to estimate the source wavelet at a different offset. For PZ summation, Barr and Sanders (1989) have derived a relation to model the up-going wavefield as shown in the following equation:

$$U(t,x) = \frac{1}{2} \left( P(t,x) + \frac{\rho v_p}{cos \gamma_p} \frac{k_t (1+k_r)}{(1-k_r)} Z(t, x) \right) ,$$ (2)

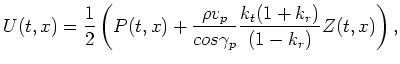where $U(t,x)$ is the up-going wavefield, $P(t,x)$ is the pressure, $Z(t,x)$ is the vertical velocity, $\rho$ is the water density, $v_p$ is the P-wave water velocity, $\gamma_p$ is the P-wave refraction angle at the sea bottom for upgoing wavefield, and $k_r$, $k_t$ are the reflection coefficient and the refraction coefficient of the ocean bottom, respectively. One drawback of equation 2 is that it assumes that the reflection coefficent of the ocean surface is -1, which is not always true. We have used a more data-driven approach in which a scaling factor between P and Z is fitted from the amplitude of their direct arrival, as described by equations 3 and 4.

From equation 2, we can see that the scaling factor in front of $Z(t,x)$ is offset-dependent. In this study, instead of calculating the scaling factor from equation 2, we fit for it from the amplitude of the pressure and vertical velocity components, time-windowed around the direct arrival:

$$U(t,x) = \frac{1}{2} \left( P(t,x) + {\rm scale} (x) z(t, x) \right),$$

$$D(t,x) = \frac{1}{2} \left( P(t,x) - {\rm scale} (x) z(t, x) \right),$$ (3)

$${\rm scale} (x) = \frac{\sum_{t \in \Omega_t} \mid P(t,x) \mid }{ \sum_{t \in \Omega_t} \mid Z(t,x) \mid },$$ (4)

where scale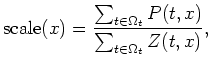$(x)$ is the offset dependent scaling factor between pressure and vertical particle velocity, and $\Omega_t$ is the time-window near the direct arrival time. Figure 7 shows the scaling factor computed using equation 4. Figure 8 shows the resulting up-going and down-going signals after PZ summation. Notice that the up-going signal is much weaker than the down going signal.

scale
Figure 7. Scaling factor as a function of offset. It is estimated from the average amplitude of P over the average amplitude of Z [ER]

PZ
Figure 8. The top shows the resulting up-going wavefields and the bottom shows the down-going wavefields after PZ summation. [ER]

Source signature and static shifts estimations for multi-component ocean bottom data