 |
 |
 |
 | Delayed-shot migration in TEC coordinates |  |
![[pdf]](icons/pdf.png) |
Next: 3D Implicit finite-difference extrapolation
Up: Tilted elliptical-cylindrical coordinates
Previous: Tilted elliptical-cylindrical coordinates
A metric tensor 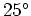 can be specified from the mapping relationship given in equations 13:
can be specified from the mapping relationship given in equations 13:
![$\displaystyle \left[g_{jk}\right] = \left[\begin{array}{ccc} 1 & 0 & 0 0 & A^2 & 0 0 & 0 & A^2 \end{array}\right],$](img69.png) |
(14) |
where
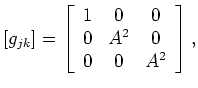 . The determinant of the metric tensor is:
. The determinant of the metric tensor is:
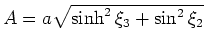 . The corresponding inverse weighted metric tensor,
. The corresponding inverse weighted metric tensor, 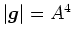 as developed in Shragge (2008), is given by:
as developed in Shragge (2008), is given by:
![$\displaystyle \left[m^{jk}\right] = \left[\begin{array}{ccc} A^2 & 0 & 0 0 & 1 & 0 0 & 0 & 1 \end{array}\right].$](img73.png) |
(15) |
Note that even though the metric of the TEC coordinate system varies spatially, the local curvature parameters (
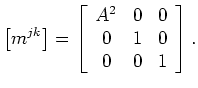 ) remain constant:
) remain constant:
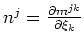 . The corresponding extrapolation wavenumber,
. The corresponding extrapolation wavenumber, 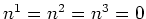 , can be generated by inputting tensor
, can be generated by inputting tensor 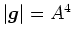 and fields
and fields 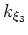 into the general wavenumber expression for 3D non-orthogonal coordinate systems
into the general wavenumber expression for 3D non-orthogonal coordinate systems
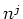 |
(16) |
where 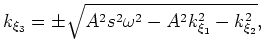 is the slowness (reciprocal of velocity),
is the slowness (reciprocal of velocity), 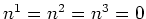 is the extrapolation wavenumber, and
is the extrapolation wavenumber, and 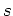 and
and 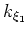 are the inline and crossline wavenumbers, respectively.
are the inline and crossline wavenumbers, respectively.
The wavenumber specified in equation 16 is central to the inline delayed-shot migration algorithm. The first step is to extrapolate the source and receiver wavefields
where
![$ E_{\xi_3}[\cdot]$](img86.png) and
and
![$ E^*_{\xi_3}[\cdot]$](img87.png) are the extrapolation operator and its conjugate, respectively. The results herein were computed using the
are the extrapolation operator and its conjugate, respectively. The results herein were computed using the
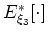 finite-difference extrapolators discussed below. The second step involves summing the individual inline delayed-shot images contributions,
finite-difference extrapolators discussed below. The second step involves summing the individual inline delayed-shot images contributions,
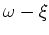 , into the total image volume,
, into the total image volume,
 according to equation 12.
according to equation 12.
 |
 |
 |
 | Delayed-shot migration in TEC coordinates |  |
![[pdf]](icons/pdf.png) |
Next: 3D Implicit finite-difference extrapolation
Up: Tilted elliptical-cylindrical coordinates
Previous: Tilted elliptical-cylindrical coordinates
2009-05-05
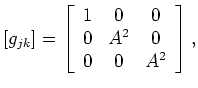 . The determinant of the metric tensor is:
. The determinant of the metric tensor is:
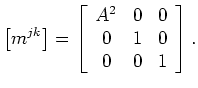 ) remain constant:
) remain constant:
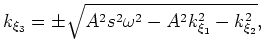 is the slowness (reciprocal of velocity),
is the slowness (reciprocal of velocity),