Next: Outlook
Up: Claerbout: Anti-crosstalk
Previous: Crosstalk in a more
For warm up we linearize in the simplest possible way.
Suppose we allow only
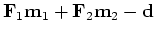 to vary keeping
to vary keeping
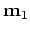 fixed.
We put
fixed.
We put
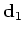 on the diagonal of a matrix, say
on the diagonal of a matrix, say
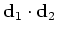 .
The regression for anti-crosstalk is now
.
The regression for anti-crosstalk is now
Define the element-by-element cross product of
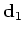 times
times
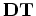 to be
to be
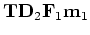 .
Now let us linearize the full non-linear
anti-crosstalk regularization.
Let a single element of
.
Now let us linearize the full non-linear
anti-crosstalk regularization.
Let a single element of
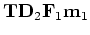 be decomposed as a base plus a perturbation
be decomposed as a base plus a perturbation
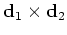 .
A single component of the vector
.
A single component of the vector
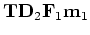 is
is
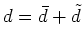 .
Linearizing the product (neglecting the product of the perturbations) gives
.
Linearizing the product (neglecting the product of the perturbations) gives
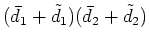 |
(8) |
This is one component. We seek an expression for all.
It will be a vector which is a product of a matrix with a vector.
We want no unknowns in matrices; we want them all in vectors
so we will know how to solve for them.
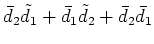 |
(9) |
Express the perturbation parts of the vectors as functions
of the model space
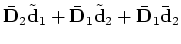 |
(10) |
This vector should be viewed under many windows (triangle shaped, for example).
Under each window we hope to see the product have a small value.
The desired anti-crosstalk regression
is to minimize the length of the vector below by variation
of the model parameters
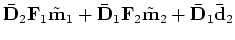 and
and
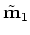 .
.
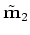 |
(11) |
This regression augments our usual regularizations.
Perhaps it partially or significantly supplants them.
Unfortunately, it requires yet another epsilon.
Upon finding
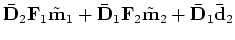 and
and
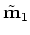 we update the base model
we update the base model
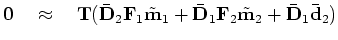 and iterate.
and iterate.
Next: Outlook
Up: Claerbout: Anti-crosstalk
Previous: Crosstalk in a more
2008-10-28
![]() to vary keeping
to vary keeping
![]() fixed.
We put
fixed.
We put
![]() on the diagonal of a matrix, say
on the diagonal of a matrix, say
![]() .
The regression for anti-crosstalk is now
.
The regression for anti-crosstalk is now
![]() times
times
![]() to be
to be
![]() .
Now let us linearize the full non-linear
anti-crosstalk regularization.
Let a single element of
.
Now let us linearize the full non-linear
anti-crosstalk regularization.
Let a single element of
![]() be decomposed as a base plus a perturbation
be decomposed as a base plus a perturbation
![]() .
A single component of the vector
.
A single component of the vector
![]() is
is
![]() .
Linearizing the product (neglecting the product of the perturbations) gives
.
Linearizing the product (neglecting the product of the perturbations) gives
![]() and
and
![]() we update the base model
we update the base model
![]() and iterate.
and iterate.