 |
 |
 |
 | Angle-domain common-image gathers in generalized coordinates |  |
![[pdf]](icons/pdf.png) |
Next: Cartesian coordinate ADCIGs
Up: ADCIG theory
Previous: ADCIG theory
Shot-profile migration in Cartesian coordinates consists of completing a recursive two-step procedure. The first step involves propagating the source and receiver wavefields, 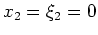 and
and 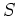 , from depth level
, from depth level
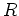 to
to 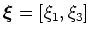 using an extrapolation operator
using an extrapolation operator
![$ E_{x_3}[\cdot]$](img16.png)
where 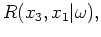 denotes the conjugate operator,
denotes the conjugate operator,  is angular frequency, and
is angular frequency, and
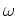 is the depth step. A subsurface image,
is the depth step. A subsurface image, 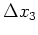 , is subsequently computed at each extrapolation step by evaluating an imaging condition
, is subsequently computed at each extrapolation step by evaluating an imaging condition
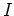 |
(2) |
where the subsurface-offset axis, 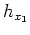 , is generated by correlating the source and receiver wavefields at various relative shifts in the
, is generated by correlating the source and receiver wavefields at various relative shifts in the 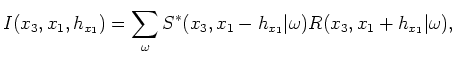 direction. Finally, the ADCIG volume is computed using an offset-to-angle transformation operator,
direction. Finally, the ADCIG volume is computed using an offset-to-angle transformation operator,
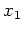
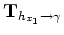 |
(3) |
where 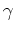 is the reflection opening angle shown in Figure 1.
is the reflection opening angle shown in Figure 1.
|
|---|
rays
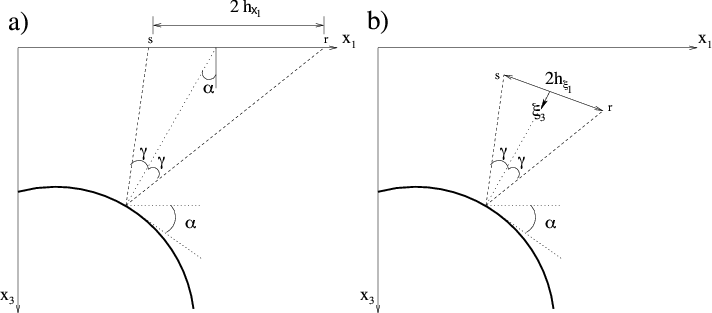
Figure 1. Cartoon illustrating the geometry of the ADCIG calculation. Parameter 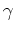 is the reflection opening angle, is the reflection opening angle, 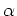 is geologic dip. a) Cartesian geometry using coordinates is geologic dip. a) Cartesian geometry using coordinates 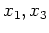 and and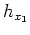 . b) Generalized geometry using coordinates . b) Generalized geometry using coordinates
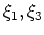 and and 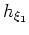 . Adapted from (). . Adapted from ().
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png)
|
|---|
Imaging in generalized coordinate systems follows the same two-step procedure. However, because of the different migration geometry in the
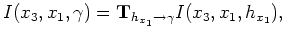 -coordinate system, new extrapolation operators,
-coordinate system, new extrapolation operators,
![$ E_{\xi_3}[\cdot]$](img31.png) , must be used to propagate wavefields. I specify these operators using Riemannian wavefield extrapolation (RWE). I do not discuss RWE herein, and refer readers interested in additional information to () and ().
, must be used to propagate wavefields. I specify these operators using Riemannian wavefield extrapolation (RWE). I do not discuss RWE herein, and refer readers interested in additional information to () and ().
The first generalized coordinate imaging step is performing wavefield extrapolation
where
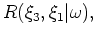 is the extrapolation step increment. Generalized coordinate images are then constructed by evaluating an imaging condition
is the extrapolation step increment. Generalized coordinate images are then constructed by evaluating an imaging condition
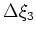 |
(5) |
where 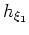 is the
is the
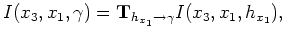 -coordinate equivalent of Cartesian subsurface offset axis
-coordinate equivalent of Cartesian subsurface offset axis 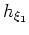 . The generalized coordinate ADCIG volume is generated by applying an offset-to-angle transformation
. The generalized coordinate ADCIG volume is generated by applying an offset-to-angle transformation
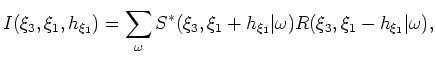
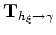 |
(6) |
Conventional ADCIG volumes can be recovered by sinc interpolating each
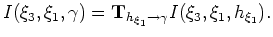 image computed via equation 6 to the final Cartesian coordinate volume.
image computed via equation 6 to the final Cartesian coordinate volume.
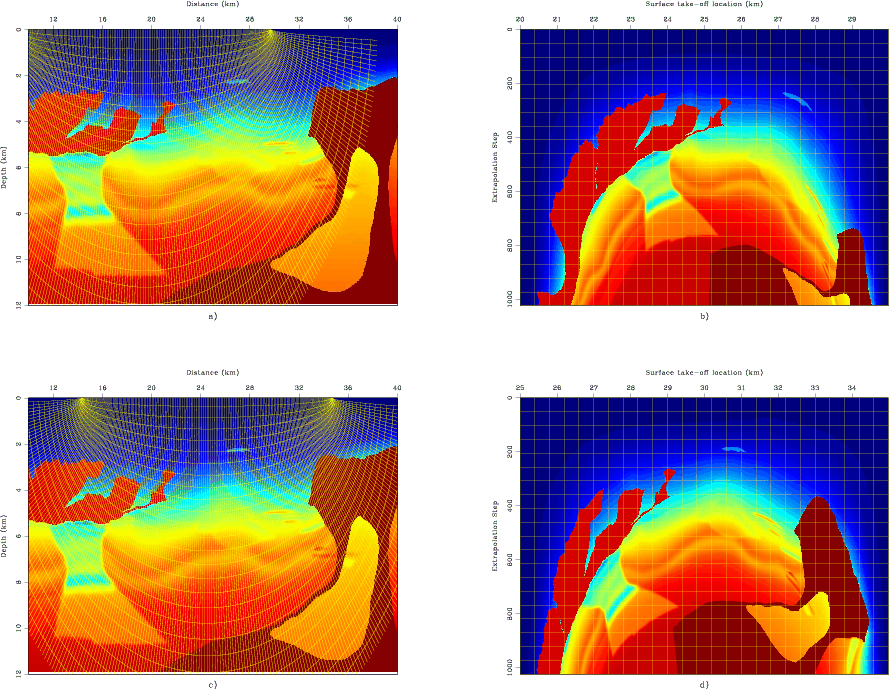
Figure 2 illustrates this process using the elliptic coordinate system. Panel 2a shows the BP synthetic velocity model (, ) with an elliptic mesh overlain. Note that the salt flanks to the right-side of the model are nearly vertical in Cartesian coordinates. Panel 2b shows the velocity model in panel 2a interpolated to the elliptic coordinate system. Importantly, the aforementioned salt flanks in the elliptic coordinate system are nearly horizontal, which should lead to ADCIG calculations more robust than in Cartesian coordinates. However, proving this assertion requires understanding the differences, if any, between the Cartesian and generalized coordinate offset-to-angle operators,
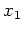 and
and
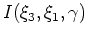 , in equations 3 and 6, respectively.
, in equations 3 and 6, respectively.
|
|---|
RC2
Figure 2. Prestack migration test in elliptic coordinates. a) Benchmark synthetic velocity model with an overlying elliptic coordinate system. b) Effective slowness model in the transformed elliptic coordinate system in a). c) Benchmark synthetic velocity model with a different overlying elliptic coordinate system. d) Effective elliptic coordinate slowness model for the coordinate system in c).
|
|---|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png)
|
|---|
 |
 |
 |
 | Angle-domain common-image gathers in generalized coordinates |  |
![[pdf]](icons/pdf.png) |
Next: Cartesian coordinate ADCIGs
Up: ADCIG theory
Previous: ADCIG theory
2009-04-13
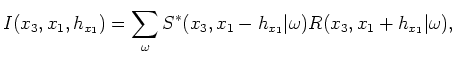 direction. Finally, the ADCIG volume is computed using an offset-to-angle transformation operator,
direction. Finally, the ADCIG volume is computed using an offset-to-angle transformation operator,

![]() -coordinate system, new extrapolation operators,
-coordinate system, new extrapolation operators,
![]() , must be used to propagate wavefields. I specify these operators using Riemannian wavefield extrapolation (RWE). I do not discuss RWE herein, and refer readers interested in additional information to () and ().
, must be used to propagate wavefields. I specify these operators using Riemannian wavefield extrapolation (RWE). I do not discuss RWE herein, and refer readers interested in additional information to () and ().
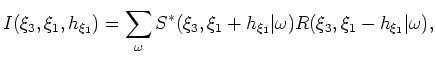
![]() and
and
![]() , in equations 3 and 6, respectively.
, in equations 3 and 6, respectively.
