|
|
|
|
Phase encoding with Gold codes for wave-equation migration |
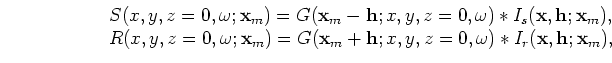 is the source wavefield and
is the source wavefield and
In the case of using an one-way extrapolator, the source and receiver wavefields are upward continued according to the one-way wave equations
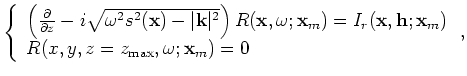 is the slowness at
is the slowness at Using the linearity of the wave propagation, sets of individual modeling experiments can be combined into the same areal data, such that the amount of data input into migration can be significantly decreased, reducing its cost. However, this procedure generates crosstalk when applying the imaging condition during migration.
Guerra and Biondi (2008) introduce strategies to attenuate the crosstalk. Migration of
![]() -random-phase encoded data disperses the crosstalk energy throughout the image as a pseudo-random background noise. By adding more realizations of random-phase encoded areal data, the speckled noise can be further attenuated. The encoded source wavefield,
-random-phase encoded data disperses the crosstalk energy throughout the image as a pseudo-random background noise. By adding more realizations of random-phase encoded areal data, the speckled noise can be further attenuated. The encoded source wavefield,
![]() , and the encoded receiver wavefield,
, and the encoded receiver wavefield,
![]() , are synthesized according to
, are synthesized according to
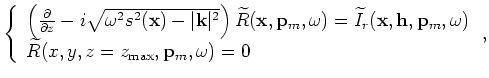 and
and
| (A-6) | |||
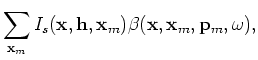 |
(A-7) |
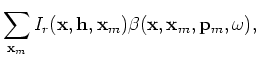 is the phase-encoding function; the variable
is the phase-encoding function; the variable
The areal shot migration is performed by downward continuation of the areal source and receiver wavefields according to the following one-way wave equations
The image,
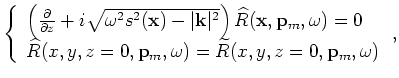 , is obtained by cross-correlation of the source wavefield,
, is obtained by cross-correlation of the source wavefield,
![]() , with the receiver wavefield,
, with the receiver wavefield,
![]()
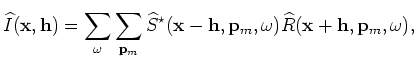 represents complex conjugation.
represents complex conjugation.
|
|
|
|
Phase encoding with Gold codes for wave-equation migration |