 |
 |
 |
 | Ignoring density in waveform inversion |  |
![[pdf]](icons/pdf.png) |
Next: Application to seismic inversion
Up: Review of waveform inversion
Previous: Review of waveform inversion
Given a solution
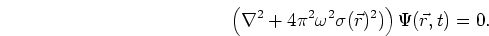 to equation (2), is it possible
to recover
to equation (2), is it possible
to recover
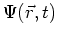 ? The Born approximation, named after physicist Max
Born, was first developed for scattering theory in quantum mechanics. Applied
to seismology, the first-order approximation provides a linear, and thus
invertible, relationship between a small change in the slowness model and a
resulting small change in the wavefield. We split the model into a background
slowness
? The Born approximation, named after physicist Max
Born, was first developed for scattering theory in quantum mechanics. Applied
to seismology, the first-order approximation provides a linear, and thus
invertible, relationship between a small change in the slowness model and a
resulting small change in the wavefield. We split the model into a background
slowness
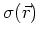 and a small slowness perturbation
and a small slowness perturbation
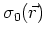 , where
, where
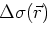 |
(3) |
The wavefield depends on slowness squared, so here we bring in the first
approximation, which is not yet the Born approximation:
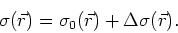 |
(4) |
To achieve an approximate relation linear with 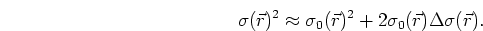 , we first
substitute (4) into the wave equation:
, we first
substitute (4) into the wave equation:
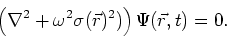 |
(5) |
This approximation is then divided into halves, with only one side depending on
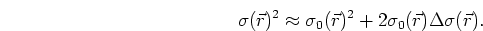 :
:
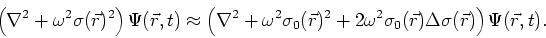 |
(6) |
Much as the slowness field was split into two parts, the wavefield now is
divided into a background wavefield 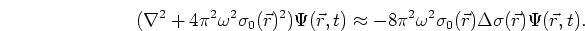 and a scattered wavefield
and a scattered wavefield
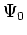 such that
such that
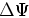 |
(7) |
where, by definition, 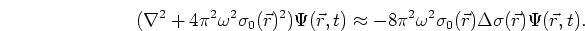 is the solution for the background wavefield, or
is the solution for the background wavefield, or
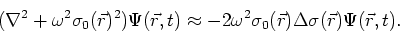 |
(8) |
Substituting the divided wavefield (7) into the approximate
wave equation (6), and using the fact that the background
wavefield is an exact solution for the background velocity, we can write
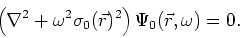 |
(9) |
At this point, we have an implicit relation between a small change
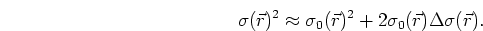 in the model and the resulting scattered wavefield
in the model and the resulting scattered wavefield 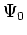 .
Ideally, we would like to have an explicit expression for
.
Ideally, we would like to have an explicit expression for 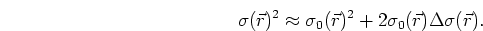 as a
function of the background and scattered wavefields. Such an expression cannot
be written directly; instead, we can find an expression for
as a
function of the background and scattered wavefields. Such an expression cannot
be written directly; instead, we can find an expression for 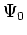 as a
function of
as a
function of 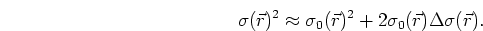 . This expression is an integral over potential
scatterers convolved with the Green's function
. This expression is an integral over potential
scatterers convolved with the Green's function
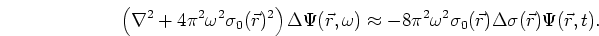 ,
the response at point
,
the response at point 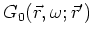 and frequency
and frequency  for a point source at
point
for a point source at
point 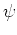 . The subscript indicates that the Green's function is defined
for the background wavefield. We build up the integral expression by starting
with the formal definition of the Green's function, which is the solution of
the wave equation with a delta-function source:
. The subscript indicates that the Green's function is defined
for the background wavefield. We build up the integral expression by starting
with the formal definition of the Green's function, which is the solution of
the wave equation with a delta-function source:
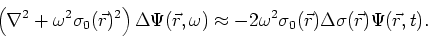 |
(10) |
Both sides of this definition are multiplied by
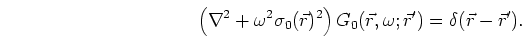 and integrated with respect to
and integrated with respect to
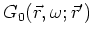 :
:
![\begin{displaymath}
-\int
d\vec{r}'2\omega^2\sigma_0(\vec{r}')\Delta\sigma(\vec...
...0(\vec{r},\omega;\vec{r}') =
\delta(\vec{r}-\vec{r}')\right].
\end{displaymath}](img28.png) |
(11) |
The Laplacian operator is taken with respect to 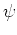 , not
, not 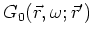 , so
the left side of the expression can be simplified by moving the integral inside
the operator; on the right side, the delta function sifts the original function
out of the integral, leaving
, so
the left side of the expression can be simplified by moving the integral inside
the operator; on the right side, the delta function sifts the original function
out of the integral, leaving
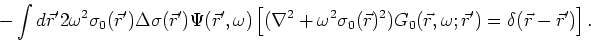 |
(12) |
Comparing with (9), we can see that the integral represents a
solution for 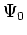 , allowing us to write
, allowing us to write
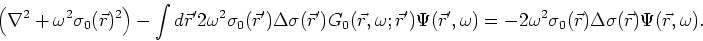 |
(13) |
Unfortunately, the scattered wavefield is still a function of the entire--and
unknown--wavefield 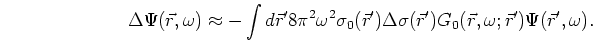 . The first-order Born approximation asserts that
when the scattered wavefield is small compared to the background wavefield, the
interaction between scattering points can be ignored. This is equivalent to
replacing
. The first-order Born approximation asserts that
when the scattered wavefield is small compared to the background wavefield, the
interaction between scattering points can be ignored. This is equivalent to
replacing 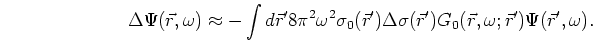 with
with 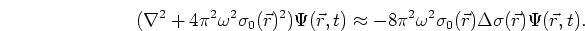 on the right-hand side, leaving
on the right-hand side, leaving
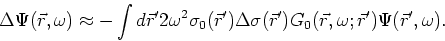 |
(14) |
This approximation now provides a linear relationship between a small change in
the model and the resulting small wavefield perturbation.
 |
 |
 |
 | Ignoring density in waveform inversion |  |
![[pdf]](icons/pdf.png) |
Next: Application to seismic inversion
Up: Review of waveform inversion
Previous: Review of waveform inversion
2007-09-18
![]() in the model and the resulting scattered wavefield
in the model and the resulting scattered wavefield ![]() .
Ideally, we would like to have an explicit expression for
.
Ideally, we would like to have an explicit expression for ![]() as a
function of the background and scattered wavefields. Such an expression cannot
be written directly; instead, we can find an expression for
as a
function of the background and scattered wavefields. Such an expression cannot
be written directly; instead, we can find an expression for ![]() as a
function of
as a
function of ![]() . This expression is an integral over potential
scatterers convolved with the Green's function
. This expression is an integral over potential
scatterers convolved with the Green's function
![]() ,
the response at point
,
the response at point ![]() and frequency
and frequency ![]() for a point source at
point
for a point source at
point ![]() . The subscript indicates that the Green's function is defined
for the background wavefield. We build up the integral expression by starting
with the formal definition of the Green's function, which is the solution of
the wave equation with a delta-function source:
. The subscript indicates that the Green's function is defined
for the background wavefield. We build up the integral expression by starting
with the formal definition of the Green's function, which is the solution of
the wave equation with a delta-function source: