Phase unwrapping of angle-domain common image gathers

Example

For a first test we create a model with a negative Gaussian anomaly in an constant velocity background (see Fig.1) and migrate (incorrectly) the modeled data using a constant velocity model. After migration we apply an offset-to-angle transformation using 33 offsets. The result is seen in Figure 2. As expected, the angle gathers show some deviation from being flat. This curvature can ideally be used to correct the migration velocity and improve the focusing. Notice the jump at near angles because of the insufficient angle sampling, a consequence of the number of processed offsets.

gath-1
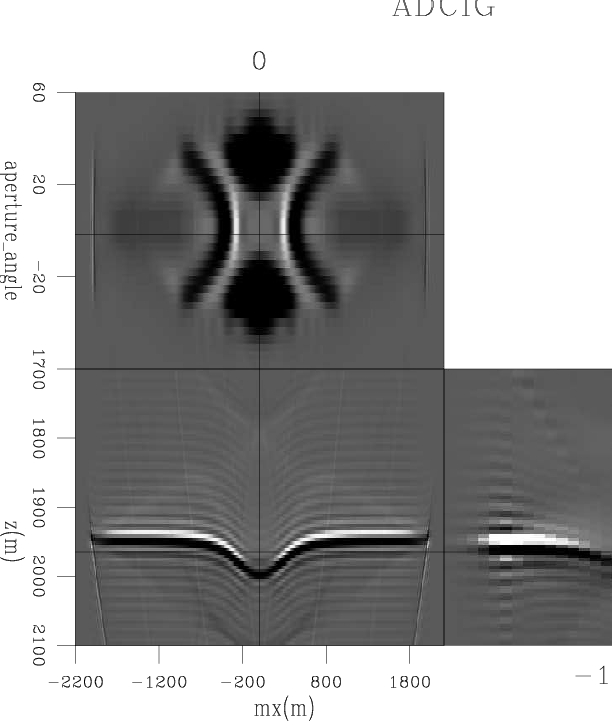
Figure 2. An Angle-Domain Common Image Gather computed using 33 offsets.

We pick 33 gathers equally spaced in the inline direction, from a position where the presence of the anomaly is unfelt to directly under the anomaly. After windowing, we tranform the $z$ axis so that for each gather we have now a kz-angle panel instead of the original $z$-angle panel. Applying the described unwrapping procedure, we obtain the result shown in Figure 3, which refers to the gather right under the anomaly.

unwrapping-33
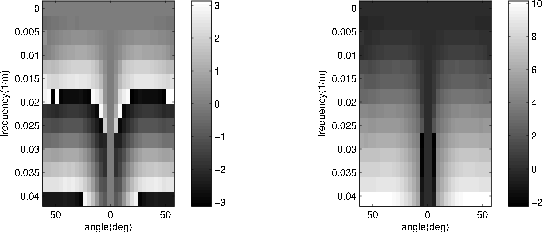
Figure 3. Wrapped (left) and unwrapped (right) phase for an ADCIG computed using 33 offsets. Phase measured in radians.

The left image is the original wrapped phase, referred to the 0 angle for visualization convenience. The right image is the corresponding unwrapped phase. Please note that the wrapped phase field is not devoid of ambiguity, i.e. the integration path is not irrelevant. However the algorithm is able to cut the phase at approximately the right position, at low angles for high frequencies. This is possible because of the choice of initial weights and the linking of several gathers together.

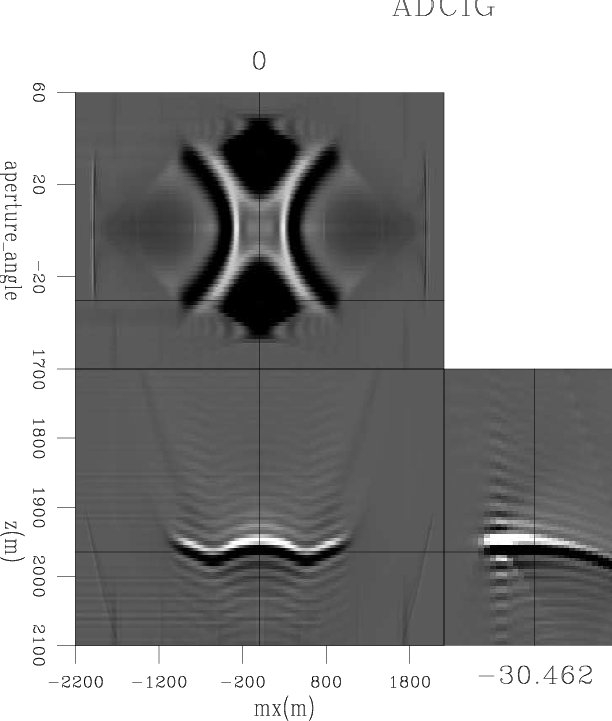
To confirm the result, we apply the same algorithm to the case where we have computed a larger number of offsets, 65 instead of 33. This increases the resolution in the angle domain (see Fig. 4), and the discontinuity disappears from the $z$-angle domain. The same happens in the kz-angle domain (see Fig. 5, left), where we no longer see a jump in the wrapped phase. The unwrapped phase is comparable to the previous one.

gath-2
Figure 4. An ADCIG computed using 65 offsets.

unwrapping-65
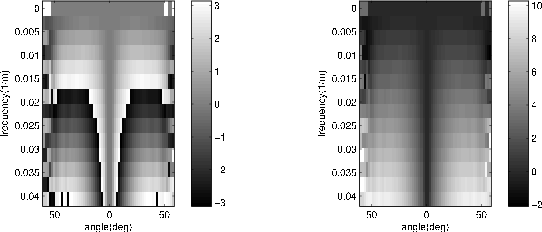
Figure 5. Wrapped (left) and unwrapped (right) phase for an ADCIG computed using 65 offsets.

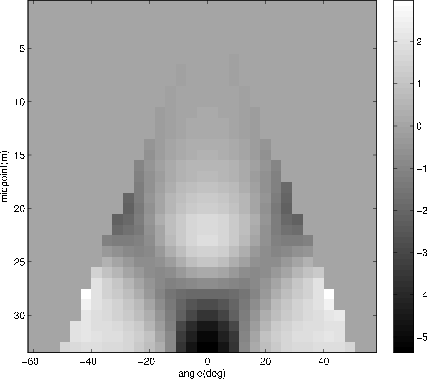
When dispersion effects can be ignored, it is possible to derive from the unwrapped phases a single number representing the delay for a given gather and a given angle. We interpolate lines into reliable unwrapped phase values, again using amplitude as a reliability criterion. The slopes of the lines correspond to the $z$-domain delays. Figures 6 and 7 display these delays in terms of samples for the two cases, with 33 and 65 offsets. For visualization purposes we subtracted the average delay for each gather, so that the effect of the anomaly is more clearly visible. A mask is used because midpoints have different angular coverage.

delay-1
Figure 6. The delay (in samples) for a number of ADCIGs as a function of aperture angle. Gathers were computed using 33 offsets.

delay-2
Figure 7. The delay (in samples) for a number of ADCIGs as a function of aperture angle. Gathers were computed using 65 offsets.

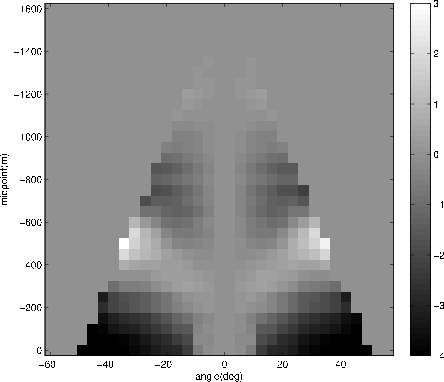
Phase unwrapping makes it possible to treat different wavenumbers independently, i.e. to take advantage of the information carried by the dispersion. Even in this simple example we can actually see some dispersion effects. Figure 8 shows the delay predicted by the single wavenumber for all gather-angle pairs, after subtraction of the ``average'' delay. Lower wavenumbers have a higher dispersion, but higher ones are more prone to unwrapping problems.

dispersion2
Figure 8. An example of the residual delay (converted to samples) for a given $kz$, after subtracting the delay identified using all wavenumbers.

Phase unwrapping of angle-domain common image gathers