 |
 |
 |
 | Angle-domain parameters computed via weighted slant-stack |  |
![[pdf]](icons/pdf.png) |
Next: Examples
Up: Guerra: Weighted offset-to-angle
Previous: Phase behavior of the
Bleistein (1987) describes a strategy to estimate parameters from the subsurface using different two images migrated with slightly different weights. Tygel et al. (1993) applied the same ideas to what they called a multiple-weight diffraction stack to obtain the stationary point location that in turn, along with source and receiver position, specifies the reflection ray. For instance, to estimate reflector dips one can compute two different migrated images,  and
and  , using two distinct migration-weighting functions, say the migration angle (
, using two distinct migration-weighting functions, say the migration angle (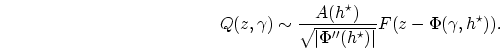 ) and simply a constant value of one (
) and simply a constant value of one (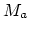 ). For
). For 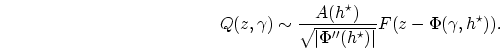 , the resulting amplitudes are weighted by the migration angles around the stationary point. In this region the migration operator and reflectors are tangent. Consequently the local average of the migration angle is an estimate of the reflector dip. So, the division
, the resulting amplitudes are weighted by the migration angles around the stationary point. In this region the migration operator and reflectors are tangent. Consequently the local average of the migration angle is an estimate of the reflector dip. So, the division  results in an estimate of the dip of the reflectors.
results in an estimate of the dip of the reflectors.
The phase behavior of the offset-to-angle transformation shows that the main contribution for the image in the angle domain comes from the vicinity of the stationary point. Therefore, the use of the weighted stacking strategy (Bleistein, 1987) to map quantities computed in the subsurface-offset domain to the angle domain is straightforward. The mapping of certain attributes can be useful, for instance, to balance amplitudes in the angle domain.
In the following, the aim of the weighted offset-to-angle transformation is to compute weights to be applied on ADCIGs in such a way that amplitude variations due to illumination are attenuated. The weighted offset-to-angle transformation is represented by the computation of ADCIGs from SODCIGs previously multiplied by some parameter -- in the present case, the subsurface-offset Hessian diagonals,  -- defined in the subsurface-offset domain. The amplitudes of the resulting ADCIGs, according to the stationary phase results in the previous section, can be represented by
-- defined in the subsurface-offset domain. The amplitudes of the resulting ADCIGs, according to the stationary phase results in the previous section, can be represented by
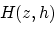 |
(9) |
where
 are the averaged values of the subsurface-offset Hessian diagonals in the vicinity of the stationary point.
The ADCIGs,
are the averaged values of the subsurface-offset Hessian diagonals in the vicinity of the stationary point.
The ADCIGs,
 , are to be divided by the non-weighted transformed results from equation 8,
, are to be divided by the non-weighted transformed results from equation 8,  , using a regularization term,
, using a regularization term,  , in the denominator to avoid division by small numbers. Finally, a median filter in the
, in the denominator to avoid division by small numbers. Finally, a median filter in the 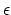 -plane (represented by
-plane (represented by
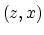 ) for every angle section is applied to remove spurious amplitudes, thus providing an estimate of subsurface-offset parameter in the angle domain.
The angle-transformed Hessian diagonals,
) for every angle section is applied to remove spurious amplitudes, thus providing an estimate of subsurface-offset parameter in the angle domain.
The angle-transformed Hessian diagonals, 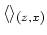 are computed according to equation 10:
are computed according to equation 10:
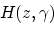 |
(10) |
The general formula of the subsurface-offset Hessian in the prestack-inversion problem is
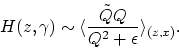 |
(11) |
where 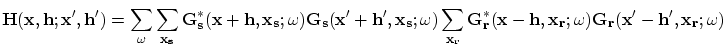 denotes Green's function from the source point,
denotes Green's function from the source point, 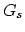 , to the image point,
, to the image point, 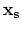 , and
, and 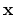 the Green's function from the image point to the receiver point,
the Green's function from the image point to the receiver point, 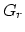 ;
; 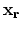 is the subsurface-offset; the prime indicates points in the image space in the vicinity of the image point and different subsurface-offsets, and the
is the subsurface-offset; the prime indicates points in the image space in the vicinity of the image point and different subsurface-offsets, and the 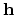 stands for the conjugate transpose of the Green's functions.
stands for the conjugate transpose of the Green's functions.
The main diagonal of the Hessian, which is the Laplacian of the cost function related to the model parameters, contains the autocorrelation of the Green's functions and, generally, carries most of the information about illumination. Sometimes, a good and cheap solution is just to approximate the Hessian by its main diagonal and apply its inverse to the migrated image. However, this procedure does not correct for kinematic errors of the migrated image and, depending on the complexity of the illumination pattern, only the least-squares inverse image may be able to provide reasonable results (Clapp, 2005).
Equation 12 shows the structure of the subsurface-offset domain Hessian used in the examples.
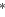 |
(12) |
In this case, the diagonals just represent the cross-correlation between Green's functions computed for a specific image point but shifted by different subsurface-offsets. The off-diagonal terms of the subsurface-offset Hessian are an expression of how much illumination for a specific subsurface-offset is conditioned by the illumination in another subsurface-offset. For the ideal case of infinite cable length, infinite frequency bandwidth and constant velocity, the subsurface-offset Hessian is the identity operator meaning that subsurface-offsets are linearly independent. In this extreme situation, all the energy in a SODCIG will be concentrated at zero-subsurface offset. Therefore, in general, the main diagonal represents an estimate of how much illumination for a specific subsurface-offset is not conditioned by the illumination in another subsurface-offset. Consequently, it is straightforward to consider the main diagonal as the natural candidate to be transformed to angle domain.
Although, in principle, any diagonal of the subsurface-offset Hessian can be transformed to the angle domain by the proposed approach, at present I have conceived a direct application only for the transformed main diagonal, which is to use it as a weight to balance the amplitudes of the ADCIGs. In the next section I show examples of the angle-domain transformed subsurface-offset Hessian diagonals, as well as the comparison of migrated images before and after the amplitude compensation with the transformed main diagonal, for a small portion of the Sigsbee dataset.
 |
 |
 |
 | Angle-domain parameters computed via weighted slant-stack |  |
![[pdf]](icons/pdf.png) |
Next: Examples
Up: Guerra: Weighted offset-to-angle
Previous: Phase behavior of the
2007-09-15
![]() -- defined in the subsurface-offset domain. The amplitudes of the resulting ADCIGs, according to the stationary phase results in the previous section, can be represented by
-- defined in the subsurface-offset domain. The amplitudes of the resulting ADCIGs, according to the stationary phase results in the previous section, can be represented by