 |
 |
 |
 | Angle-domain parameters computed via weighted slant-stack |  |
![[pdf]](icons/pdf.png) |
Next: Weighted offset-to-angle transformation
Up: Guerra: Weighted offset-to-angle
Previous: Introduction
The offset-to-angle transformation can be expressed by the integration of the subsurface-offset domain common image gathers (SODCIGs),  , along a certain slanted path, according to the equation
, along a certain slanted path, according to the equation
![\begin{displaymath}
Q(z,\gamma) = \int_{A} \varrho[P(z,h)] dh \arrowvert_{z = \zeta(\gamma,h) } ,
\end{displaymath}](img3.png) |
(1) |
where  is the output ADCIG,
is the output ADCIG, 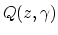 is depth,
is depth, 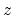 is the aperture angle,
is the aperture angle, 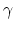 is the subsurface offset,
is the subsurface offset, 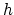 is the rho-filter which aims to yield the correct phase of the output ADCIG (, ),
is the rho-filter which aims to yield the correct phase of the output ADCIG (, ), 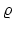 is the domain of integration that defines the range of subsurface offsets to be summed, and
is the domain of integration that defines the range of subsurface offsets to be summed, and
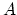 is the slanted path given by
is the slanted path given by
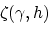 |
(2) |
where  is the depth coordinate at zero subsurface offset. A single reflector in a SODCIG can be represented by
is the depth coordinate at zero subsurface offset. A single reflector in a SODCIG can be represented by
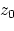 |
(3) |
where  is an amplitude term whose value depends on the reflection coefficient, illumination and focusing,
is an amplitude term whose value depends on the reflection coefficient, illumination and focusing, 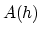 is the depth domain representation of the seismic pulse, and
is the depth domain representation of the seismic pulse, and 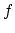 is the reflector depth. The fact that
is the reflector depth. The fact that 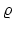 and
and 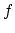 are functions of
are functions of 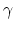 accommodates the focusing of reflector amplitudes at nonzero-subsurface offsets because of inaccuracies in migration velocity and problems in illumination. A SODCIG containing several reflectors can be described by the superposition of individual reflectors, each described by equation 3.
accommodates the focusing of reflector amplitudes at nonzero-subsurface offsets because of inaccuracies in migration velocity and problems in illumination. A SODCIG containing several reflectors can be described by the superposition of individual reflectors, each described by equation 3.
Equation 1, Fourier transformed to the 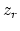 domain after inserting equation 3, reads
domain after inserting equation 3, reads
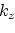 |
(4) |
where
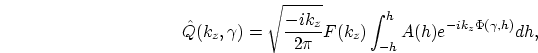 is the phase function. Assuming that
is the phase function. Assuming that  is not itself an oscillating function, and considering the high-
is not itself an oscillating function, and considering the high-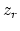 regime, the argument of the integral in equation 4 rapidly oscillates, yielding negligible amplitudes for integration over a full period, except for the case where the phase function,
regime, the argument of the integral in equation 4 rapidly oscillates, yielding negligible amplitudes for integration over a full period, except for the case where the phase function,
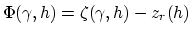 , remains stationary. This condition is achieved in the vicinity of a point -- the stationary point -- in the SODCIG with a certain subsurface offset,
, remains stationary. This condition is achieved in the vicinity of a point -- the stationary point -- in the SODCIG with a certain subsurface offset, 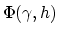 , where
, where
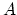 is tangent to
is tangent to 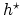 , or
, or
estimated in  .
.
Equation 4 can be evaluated by the stationary-phase method. According to Bleistein (1984), under the assumption of a single stationary point in which the second derivative does not vanish, integrals like
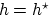 |
(5) |
where  is a smooth and compact function, can be asymptotically approximated by
is a smooth and compact function, can be asymptotically approximated by
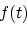 |
(6) |
if
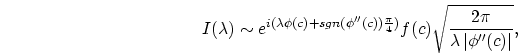 . The term
. The term
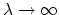 corresponds to the signal of the second derivative of the phase function,
corresponds to the signal of the second derivative of the phase function, 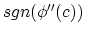 , evaluated at the stationary point,
, evaluated at the stationary point, 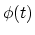 .
.
It turns out that the stationary phase formula of equation 4 is given by
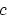 |
(7) |
Finally, the inverse Fourier transform of equation 7 gives
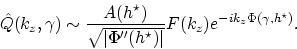 |
(8) |
Equation 8 shows that the main contribution to the amplitudes in the ADCIG comes from the vicinity of the stationary point. The second derivative of the phase function with respect to 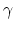 is basically the second derivative of
is basically the second derivative of 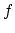 , as
, as
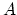 is a straight line. If
is a straight line. If 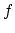 is a straight event in the SODCIG, meaning that just a very small range of angles has been illuminated (Tang, 2007), there will be as many stationary points as subsurface offsets. In this situation, the integration interval is divided in such a way that each new interval contains only one stationary point, and the final result is the sum of all individual stationary point contributions. The other special case is when all the energy is focused at zero subsurface-offset, indicating good illumination for all reflection angles and migration with the correct velocity. It is a generalization of the previous case and is solved in the same way for various illumination angles.
is a straight event in the SODCIG, meaning that just a very small range of angles has been illuminated (Tang, 2007), there will be as many stationary points as subsurface offsets. In this situation, the integration interval is divided in such a way that each new interval contains only one stationary point, and the final result is the sum of all individual stationary point contributions. The other special case is when all the energy is focused at zero subsurface-offset, indicating good illumination for all reflection angles and migration with the correct velocity. It is a generalization of the previous case and is solved in the same way for various illumination angles.
 |
 |
 |
 | Angle-domain parameters computed via weighted slant-stack |  |
![[pdf]](icons/pdf.png) |
Next: Weighted offset-to-angle transformation
Up: Guerra: Weighted offset-to-angle
Previous: Introduction
2007-09-15
![]() , along a certain slanted path, according to the equation
, along a certain slanted path, according to the equation
![]() domain after inserting equation 3, reads
domain after inserting equation 3, reads
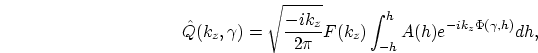 is the phase function. Assuming that
is the phase function. Assuming that  .
.
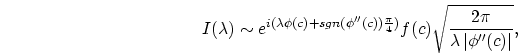 . The term
. The term