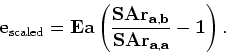|
 |
 |
 | Prediction error filters to enhance differences |  |
![[pdf]](icons/pdf.png) |
Next: Precision
Up: R. Clapp: PEF enhancement
Previous: Methodology
The previous section discussed a covariance-based approach to compare two volumes.
In this section I will discuss a more tradition amplitude-based approach.
Strict differences between the volumes is an option in some instances but often
approaches have significantly different amplitude profiles. One solution is
called histogram equalization.
My implementation of this approach is to
first calculate the amplitude in volume `a' at several different quantiles
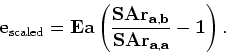 |
(6) |
where  is the amplitude at a given percentile
is the amplitude at a given percentile 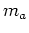 of volume
of volume 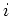 using
the quantile function
using
the quantile function 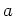 . The vector
. The vector  is basically a discrete
version of the data's cumulative distribution function (CDF).
I then found the amplitude in volume `b' at the same quantiles producing
the amplitude map
is basically a discrete
version of the data's cumulative distribution function (CDF).
I then found the amplitude in volume `b' at the same quantiles producing
the amplitude map 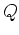 . Figure 5 shows the cumulative
distribution function for the one and eight velocity PSPI migrations shown
in the previous section.
Note how the two curves are similar, diverging only at their edges. Finally
I looped through volume `b', for each sample I found its approximate quantile by finding
the samples of
. Figure 5 shows the cumulative
distribution function for the one and eight velocity PSPI migrations shown
in the previous section.
Note how the two curves are similar, diverging only at their edges. Finally
I looped through volume `b', for each sample I found its approximate quantile by finding
the samples of 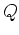 that contained the value and performing linear interpolation.
I was able to remap into the amplitude profile of `a' using
that contained the value and performing linear interpolation.
I was able to remap into the amplitude profile of `a' using  .
Figure 6 shows the difference between the one and eight
reference velocity PSPI migration after histogram normalization. Note the image
seems to emphasize the major reflectors of the image rather than the differences.
.
Figure 6 shows the difference between the one and eight
reference velocity PSPI migration after histogram normalization. Note the image
seems to emphasize the major reflectors of the image rather than the differences.
cdf
Figure 5. The solid curve is the CDF for the eight velocity PSPI
migration shown in Figure 1, the dashed curve shows the CDF using
one velocity (shown in Figure 3). Note how the two curves are similar diverging
only at their edges.
|

|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png)
|
|---|
onevel-diff
Figure 6. The difference between the one and eight
reference velocity PSPI migration after histogram normalization.
|

|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png)
|
|---|
 |
 |
 |
 | Prediction error filters to enhance differences |  |
![[pdf]](icons/pdf.png) |
Next: Precision
Up: R. Clapp: PEF enhancement
Previous: Methodology
2007-09-18