Accelerating seismic computations using customized number representations on FPGAs

Downward continued based migration

For downward continued based migration there are four potential computational bottlenecks that vary depending on the flavor of the downward continuation algorithm. In many cases the dominant cost is the FFT step. The dimensionality of the FFT varies from 1-D (tilted plane-wave migration (Shan and Biondi, 2007)) to 4-D (narrow azimuth migration (, ). The FFT cost is often dominant due its 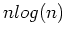$nlog(n)$ cost ratio, 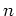$n$ being the number of points in the transform, and the non-cache friendly nature of multi-dimensional FFTs. The FK step, which involves evaluating a square root function and performing complex exponential is a second potential bottleneck. The high operational count per sample can eat up significant cycles. The FX step, which involves a complex exponential, or sine/cosine multiplication, has a similar, but computationally less demanding, profile. Creating subsurface offset gathers for shot profile or plane-wave migration, particularly 3D subsurface offset gathers, can be an overwhelming cost. The large op-count per sample and the non-cache friendly usage can be problematic. Finally, for finite difference based schemes a significant convolution cost is involved.

Last summer the focus was on speeding up 1 and 2-D FFTs. Speedup ranged from 8x-16x depending on the required data precision. (Pell and Clapp, 2007) demonstrated that the subsurface offset calculation can be sped up by a factor of 20x-40x. This summer, the focus was speeding up the FK step by implementing both a table lookup and complex exponential on the FPGA.

Accelerating seismic computations using customized number representations on FPGAs