Accelerating seismic computations using customized number representations on FPGAs

Case Study II: Convolution

To test the speedup potential for reverse time migration we implemented a 6th order acoustic modeling kernel. The 3D convolution uses a kernel with 19 elements. Once each line of the kernel has been processed, it is scaled by a constant factor. We extend the approach to the 2D convolution used last year which works by indexing into the stream to obtain values already sent to the FPGA. These values are stored in BRAM FIFOs, automatically generated and assigned by ASC. The convolution was tested on a data size of $700 \times 700 \times 700$.

The main reason for a speedup is that the processor has limited computational resources. Furthermore, the processor uses floating-point units as opposed to fixed-point units. We exploit the parallelism of the FPGA to calculate one result per cycle. When ASC assigns the elements to BRAMs it does so in such a way as to maximize the number of elements that can be obtained from the BRAM every cycle. This means that consecutive elements of the kernel must not in general be placed in the same BRAM. Since we can use variable precision, we reduce the computation overhead, increasing the throughput. To compute the entire computation all at the same time (as is the case when a high-performance processor is used) requires a large local memory (in the case of the processor, a large cache). The FPGA has limited resources on-chip (376 BRAMs which can each hold 512 32-bit values). To solve this problem we break the large data-set into cubes. To utilize all of our input and ouput bandwidth, we assign 3 processing cores to the FPGA resulting in 3 inputs and 3 outputs per cycle at 125MHz (constrained by the throughput of the PCI-Express bus). This gives us a theoretical maximum throughput of 375M results a second.

The disadvantage to breaking the problem into smaller blocks is that the boundaries of each block are essentially wasted (although a minimal amount of reuse can occur) because they must be reused when the adjacent block is calculated. We do not consider this a problem since the blocks we use are at least $100 \times 100 \times 700$ which means only a small proportion of the data is resent. The amount of BRAM assigned to each block is calculated as follows:

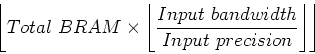$$\left \lfloor Total BRAM \times \left \lfloor \frac{Input bandwidth}{Input precision} \right \rfloor \right \rfloor$$ (4)

which assumes that the output precision is the same as the input precision. From this we can work out the size of the block. In our case we get $\lfloor 376 * \lfloor (64 / 21) \rfloor \rfloor = 125$. Due to the number of multipliers and adders required, we cannot fit 3 cores onto the FPGA directly because the number of slices used would be too high. If all of the operations are assigned to the DSP blocks we wouldn't have enough. We therefore choose a hybrid approach in which we break each multiply into 2 parts. We use one 18-bit hard multiplier (1 DSP block) and put the rest of the calculation (3 smaller multipliers) directly into logic.

In software, the convolution we try to accelerate executes in 11.2 seconds on average. The experiment was carried out using a dual-processor machine (each quad-core Intel Xeon 1.86GHz) with 8GB of memory.

In hardware, using the MAX-1 platform we obtain a 5 times speedup. The design uses 48 DSP blocks (30%), 369 (98%) RAMB16 blocks and 30,571 (72%) of the slices on the Virtex -4 chip. This means that there is room on the chip to substantially increase the kernel size. For a larger sized kernel (31 points) the speedup should be virtually linear resulting in a 8x speedup compared to the CPU implementation.

Accelerating seismic computations using customized number representations on FPGAs